 Coffee Space
Coffee Space 
In a previous post where I released uDatabase, I discussed the important of good hashing and how it really helped with the speed of my database library.
But that go me thinking: How do I really know what I have done is better?
My use-case is somewhat unique compared to other example hash functions, as I need to be able to do the following:
char* arbitrary length to a
char* of fixed length.Use looks something like so:
0001 char* key = "some value"; 0002 char hash[16]; 0003 func(key, hash, 16); 0004 uint16_t shortHash = *(uint16_t*)hash; 0005 /* Do something with values */
Why? The first two bytes are used as a shorter hash for a look-up table to reduce searching, whereas the rest of the hash is simply to confirm that a given key is unique if the initial check passes. This greatly reduces computation. Bare in mind, this hash function may be run millions of times a second!
Whilst searching on the wild world web I found this article by Andrei Ciobanu on Implementing Hash Tables in C. He kindly offers his source code which was an inspiration for my testing.
Unfortunately I was unable to use his code or testing, as he was
interested in handling hash functions that return uint32_t
and I am interested in char*, as well as wanting to
visualize the quality of the hashes and benchmark the performance. I
therefore took the time to write my own tests.
I created a small piece of checking code here. It outputs results, as well as various visualisation in PGM format. There is then a script to convert the PGM files to scaled JPG files (which are displayed here). The idea is to be able to visualise the collisions of the hash function, and therefore the quality. Black areas mean large numbers of collisions, whereas white means lower numbers of collisions.
In these tests, I test the collisions for uint8_t,
uint16_t and “uint24_t” (which doesn’t exist).
This in turn gives us single-byte and two-byte collisions, whereas the
three-byte collisions indicate the hashing quality after the initial
concentration area.
Why not test more bytes for collisions? The problem is storing the collisions in RAM. These tables are already quite large! The program already consumes in excess of 500MB of RAM during testing and each additional bit to be tested doubles that!
I’ll start off by giving the main results (lower is better):
| func | ms | col=8 | col=16 | col=24 |
|---|---|---|---|---|
| cust1 | 2634 | 16777200 | 16776960 | 16773120 |
| cust2 | 2839 | 16777001 | 16773120 | 16711680 |
| cust3 | 2993 | 16776960 | 16711680 | 15902144 |
| cust4 | 2295 | 16776960 | 16711680 | 15741061 |
We check keys (16777216). We expect that for a single byte, there is no way to avoid a collision. As we increase the number of bytes, good hashing algorithms will decrease the number of collisions.
As you can see, the hashing function named cust4 runs
faster and has the least collisions in each scenario.
This was my initial “make something work” function. It did an ‘okay job’ during initial testing.
0006 char* hash_cust1(char* s, char* d, int n){
0007 int x = -1;
0008 while(s[++x]) d[x % n] = s[x] ^ (x < n ? '\0' : d[x % n] << 2);
0009 while(x < n) d[x++] = '\0';
0010 return d;
0011 }
Performance: In terms of performance, this was my second best forming algorithm. We pay heavily for the inline ternary operator and this for sure affects branch prediction.
Collisions: This was awful.
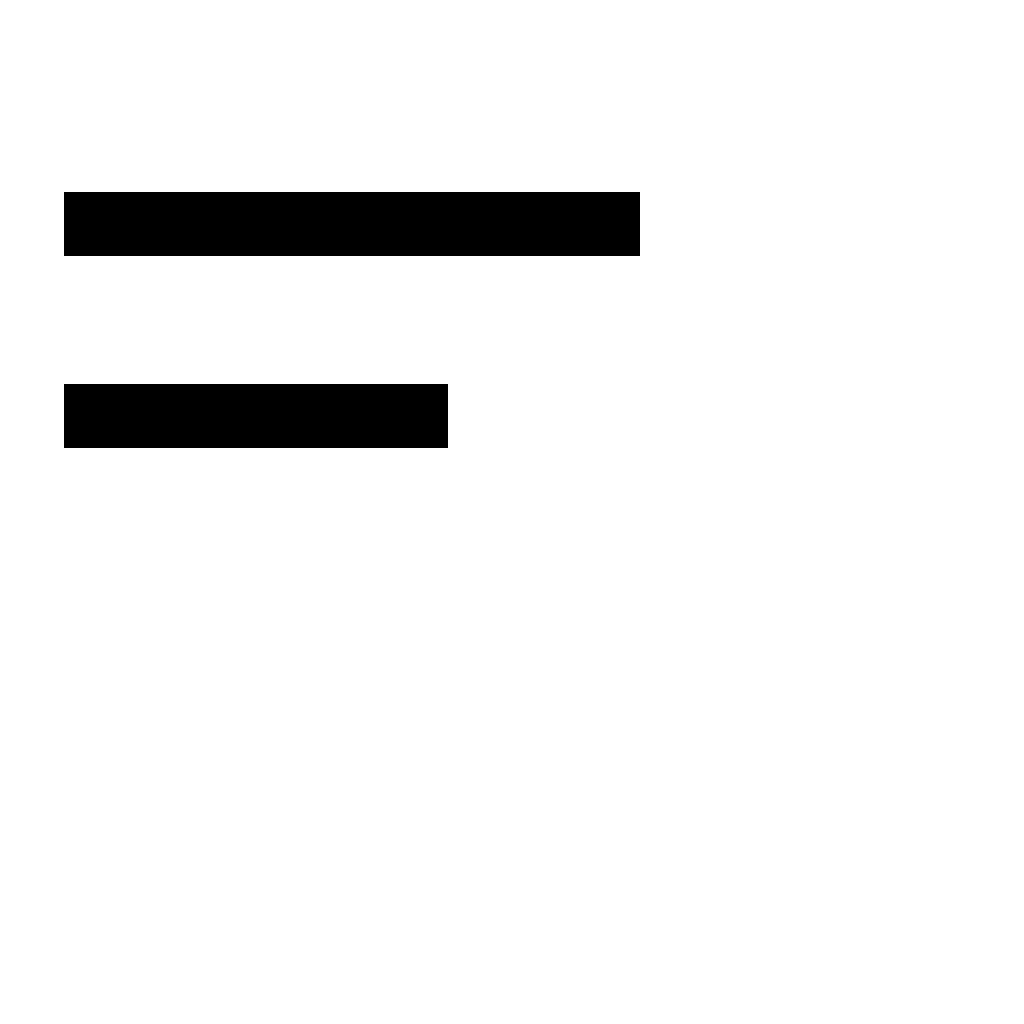
As can be seen in the one-byte output, the function was completely
unable to hash char characters with large overlap.

The two-byte output shows how insanely bad this problem is, with collisions typically happening in exactly the same locations.

It obviously doesn’t improve as we look towards three-byte output. I late realised it is even worse than I thought. If , it overrides any previous good effort attempt to hash the first two bytes. Ouch!
At this time I has realised that my hashing function was significantly holding back my program, so I looked to make some small changes to improve test results.
0012 char* hash_cust2(char* s, char* d, int n){
0013 int x = -1;
0014 while(s[++x]) d[x % n] = s[x] ^ (s[x + 1] << 3);
0015 while(x < n) d[x++] = '\0';
0016 return d;
0017 }
Performance: We managed to lose the ternary
operator, so things were looking good! But - for some reason, this
actually decreased performance. I imagine there was some cost to looking
one byte into the future and performing some operation on it with the
current byte. Perhaps there is some cost associated with accessing
memory more than once. I would imagine that s[x + 1] would
be kept in a register for the next loop, but clearly not?
Collisions: It’s still not great, but clearly a massive improvement!
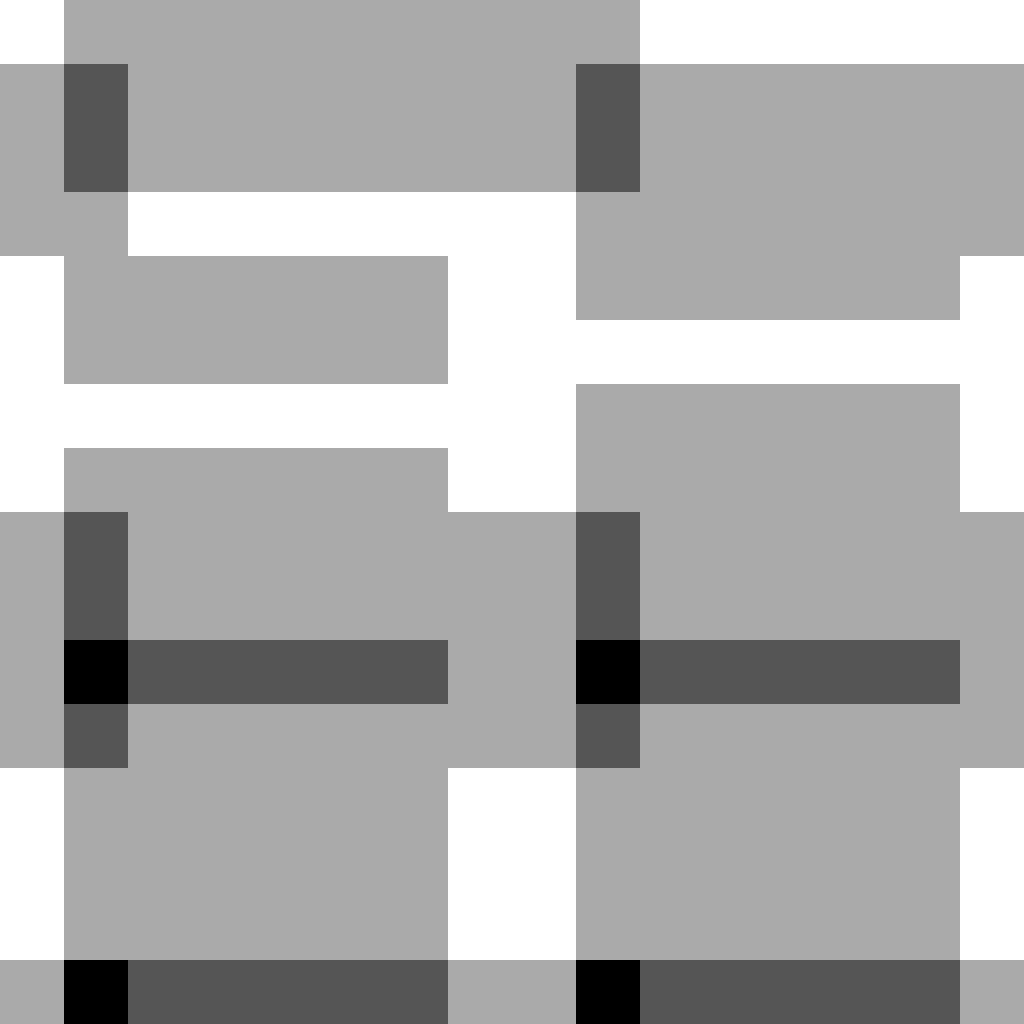
As we can see, the one-byte output is now more spread out! It’s still a very repeatable, not very well spread pattern - but this is a remarkably better distribution.

Unfortunately this didn’t hold up as we look at the two-byte output. It’s still a much better distribution, but not great.
One thing this function does well is to scatter the distribution
across the entire range. This is where we see that s[x + 1]
come into its own - but again it is too costly.
It’s now that I decided to focus more heavily on the entropy of those first two bytes, where here is achieved by having a dedicated line just for hashing those first two bytes repeatedly.
0018 char* hash_cust3(char* s, char* d, int n){
0019 int x = -1;
0020 while(s[++x]){
0021 d[x % n] = s[x];
0022 d[x % sizeof(uint16_t)] ^= s[x] << 3;
0023 }
0024 while(x < n) d[x++] = '\0';
0025 return d;
0026 }
Performance: As a result of this extra dedicated operation, we lose performance. For the purpose of the application though, this was worth it, as it reduced collisions and therefore increased overall performance.
Collisions: Collisions are tonnes better in this version! It’s night and day!
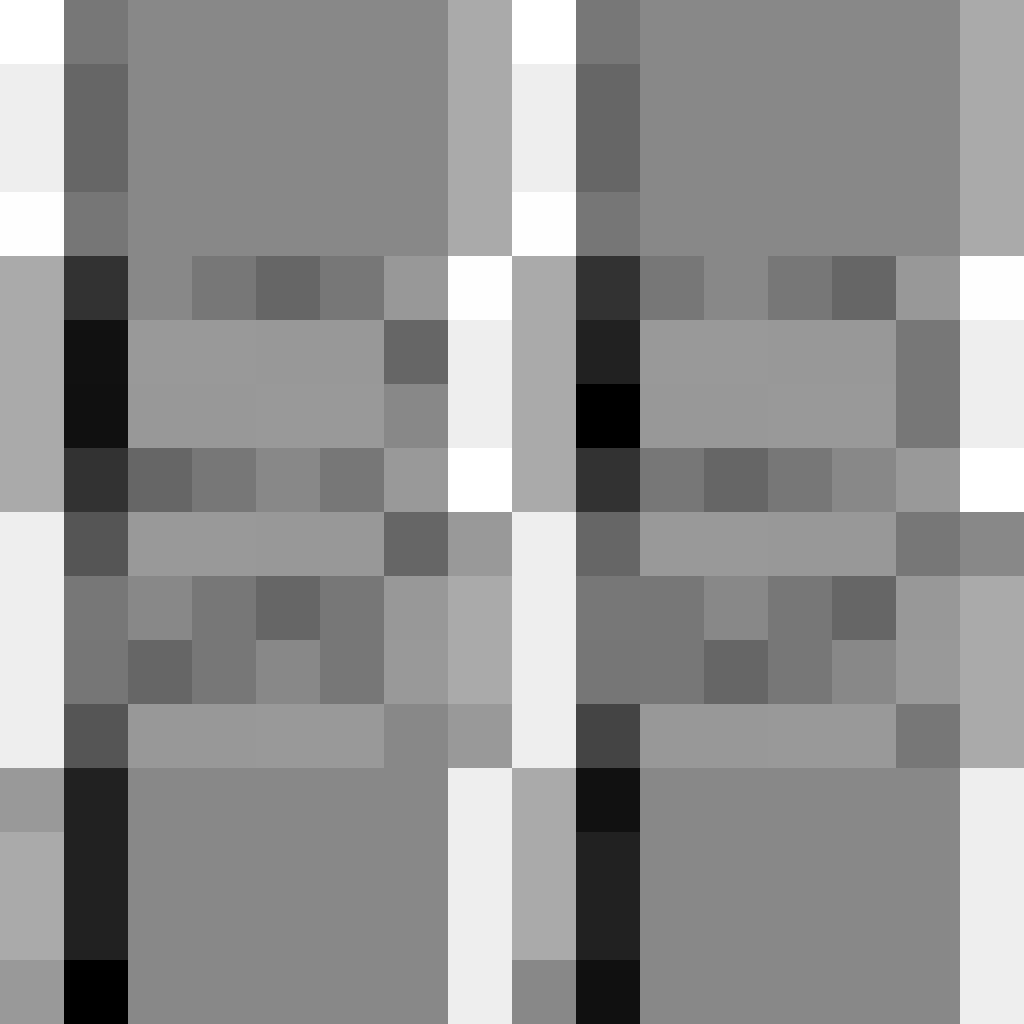
As you can see, for one-byte we have a much better spread, but still not perfect.
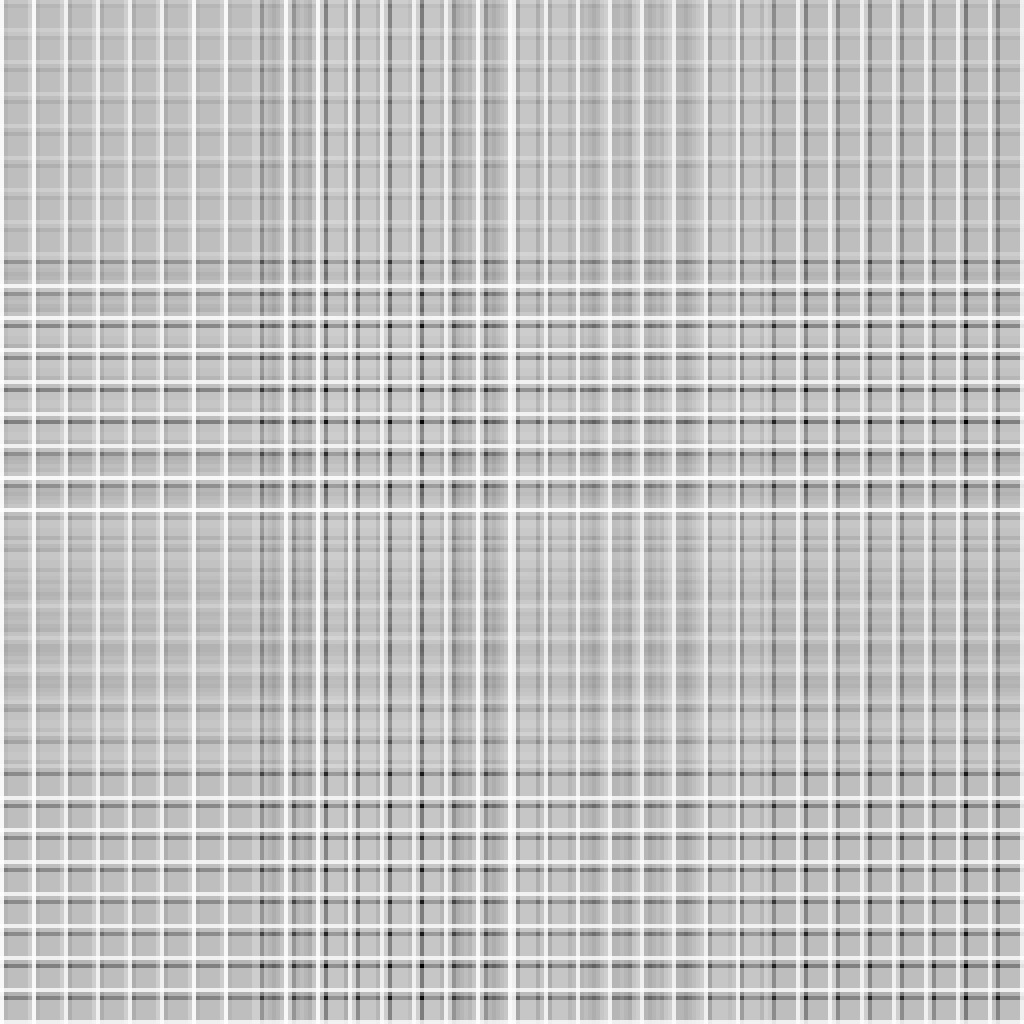
This is also the best two-byte output (so far) as we now see
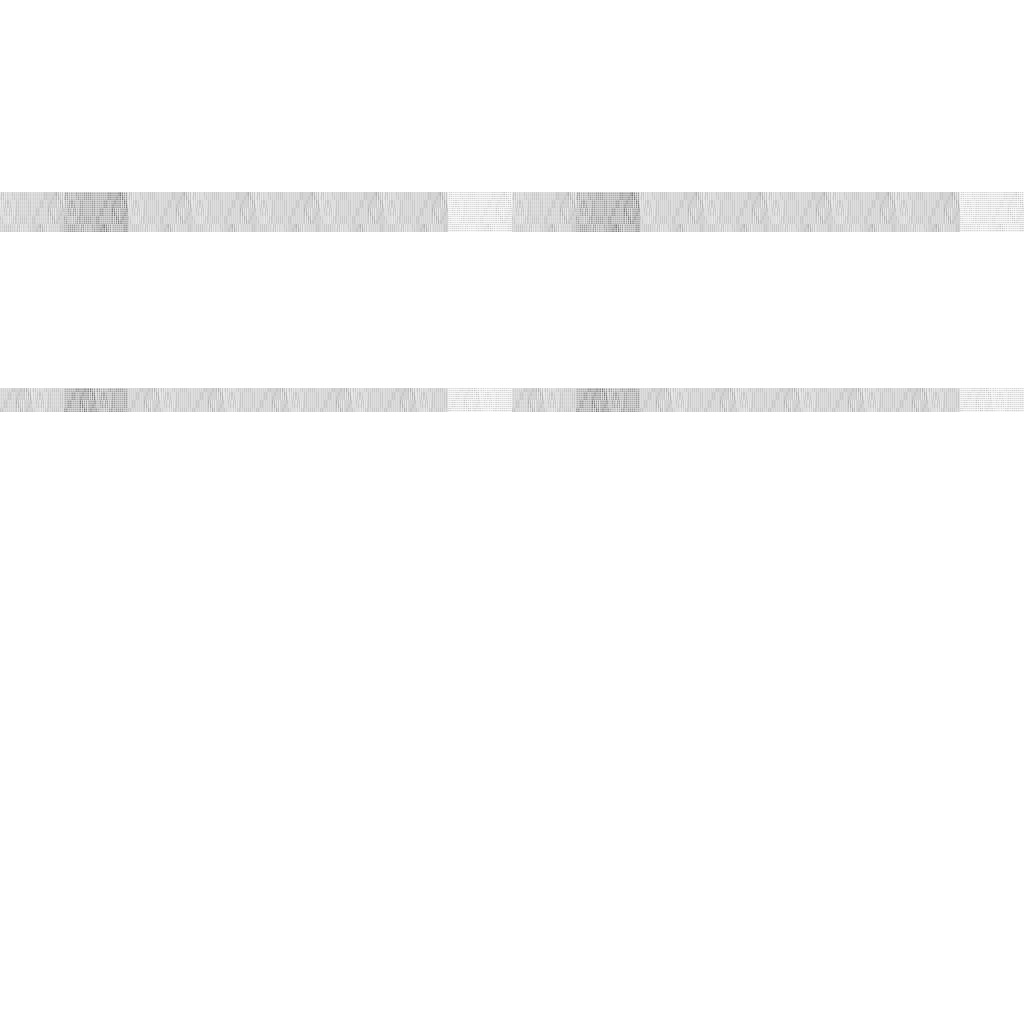
This is the ‘best’ function I could derive based on function 3
(cust3). It now uses memset to zero out the
memory, which means a bunch of optimizations methods can be used to
accelerate the zeroing of this space. Additionally everything is
in-lined to increase simplicity.
0027 char* hash_cust4(char* s, char* d, int n){
0028 memset(d, 0, n);
0029 for(int x = 0; *s; ++x) *(int16_t*)d = (*(int16_t*)d << 5) ^ *(int16_t*)d + (d[x % n] ^= *s++);
0030 return d;
0031 }
Performance: The performance is better than function
3 (cust3), but not as as good as the functions before.
Collisions: The number of collisions are reduced, but not significantly. You can see there is a very visible pattern in the visualisation and this this will ultimately cause larger numbers of hash collisions.
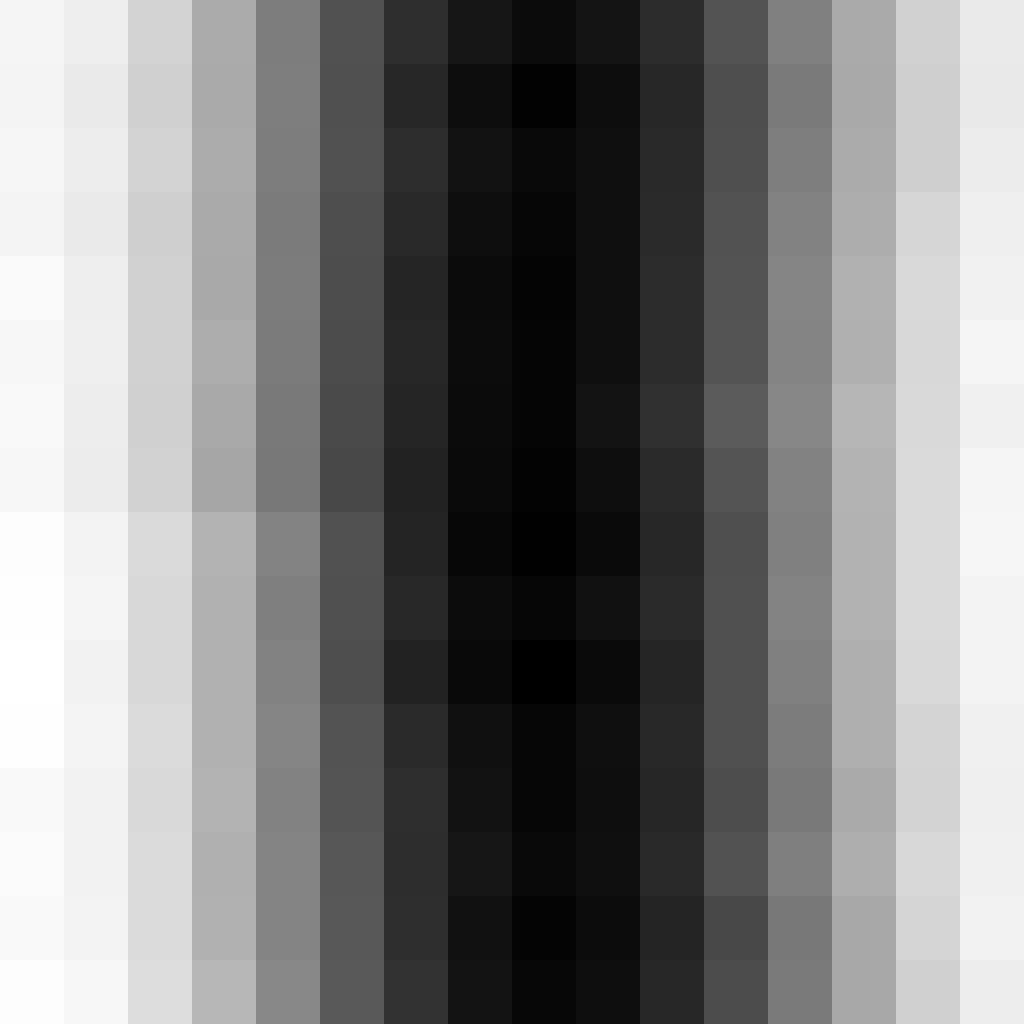
The one-byte spread clearly has a pattern, but this is significantly better than previous attempts.

The two-byte pattern is clearly much better than all previous attempts - we can now be certain that hashes are distributed over the entire space.

The thee-byte visualisation shows that we still suck at distributing the data over multiple bytes. The entropy is entirely concentrated on the first two bytes.
Ideally, we want a faster function that reduces collisions with the exact same data. Is this possible? Yes.
Armed with this new knowledge, I now test some new functions (and display the results for previous algorithms during the same run window) for keys:
| func | ms | col=8 | col=16 | col=24 |
|---|---|---|---|---|
| cust1 | 4267 | 16777200 | 16776960 | 16773120 |
| cust2 | 4506 | 16777001 | 16773120 | 16711680 |
| cust3 | 5292 | 16776960 | 16711680 | 15902144 |
| cust4 | 4712 | 16776960 | 16711680 | 15741061 |
| cust5 | 4602 | 16776960 | 16711680 | 15730195 |
| cust6 | 4761 | 16776960 | 16711680 | 15728390 |
| cust7 | 4265 | 16776960 | 16711680 | 15632352 |
| cust8 | 4468 | 16776960 | 16711680 | 15728624 |
| cust9 | 6168 | 16776960 | 16711680 | 6155480 |
| cust10 | 5329 | 16776960 | 16711680 | 6138576 |
| cust11 | 5320 | 16776960 | 16711680 | 7083260 |
| cust12 | 4988 | 16776960 | 16711680 | 5915585 |
| cust13 | 4838 | 16776960 | 16711680 | 5915585 |
As you can see, cust12 and cust13 have the
least hash collisions whilst maintaining respectable timing (compared to
the cust4 benchmark).
And for the purpose of really exaggerating the timing, I run them also at keys (268435456):
| func | ms | col=8 | col=16 | col=24 |
|---|---|---|---|---|
| cust1 | 68992 | 268435440 | 268435200 | 268431360 |
| cust2 | 74341 | 268435241 | 268431360 | 268369920 |
| cust3 | 78551 | 268435200 | 268369920 | 267386624 |
| cust4 | 70847 | 268435200 | 268369920 | 267386624 |
| cust5 | 66663 | 268435200 | 268369920 | 267386644 |
| cust6 | 82937 | 268435200 | 268369920 | 267386624 |
| cust7 | 65465 | 268435200 | 268369920 | 261502963 |
| cust8 | 65944 | 268435200 | 268369920 | 267386864 |
| cust9 | 81174 | 268435200 | 268369920 | 251658253 |
| cust10 | 76063 | 268435200 | 268369920 | 251658241 |
| cust11 | 71695 | 268435200 | 268369920 | 251658302 |
| cust12 | 66548 | 268435200 | 268369920 | 251658240 |
| cust13 | 66037 | 268435200 | 268369920 | 251658240 |
As you can see, cust5, cust7,
cust8, cust12 and cust13 all
outperform cust14. We’ll now go into a little more detail
about the algorithms and how they were designed…
This is similar the function 4, but operates on the theory that we
are shifting our entropy out the front of the uint16_t.
Instead of shifting by 5, we instead shift by 3:
0032 char* hash_cust5(char* s, char* d, int n){
0033 memset(d, 0, n);
0034 for(int x = 0; *s; ++x) *(int16_t*)d = (*(int16_t*)d << 3) ^ *(int16_t*)d + (d[x % n] ^= *s++);
0035 return d;
0036 }
Shifting by lower values seems to reduce the number of clock-cycles required to do the shift. Ideally shift values should be as low as possible.
Performance: As can bee seen, we reduce the running
time when compared to function 4 (cust4).
Collisions: We perform slightly worse on collisions, but it is worth the speed-up.

The one-byte pattern looks very good. No place in particular looks overly concentrated.

This scales well to the two-byte pattern where we see a relatively nice distribution. At this point I realised that the blocky-ness acutally comes from that XOR operation which can be addressed in the future!

Three-byte pattern still have really poor hash distribution and is causing tonnes of collisions.
With function 6 (cust6) I experimented with using
rotl16 instead of shift, my theory being that we were
shifting entropy straight off the bit.
0037 char* hash_cust6(char* s, char* d, int n){
0038 memset(d, 0, n);
0039 for(int x = 0; *s; ++x) *(int16_t*)d = rotl16(*(int16_t*)d, 5) ^ *(int16_t*)d + (d[x % n] ^= *s++);
0040 return d;
0041 }
Performance: Using the in-line function took a massive performance hit!
Collisions: It made only a little difference to the number of collisions ultimately.
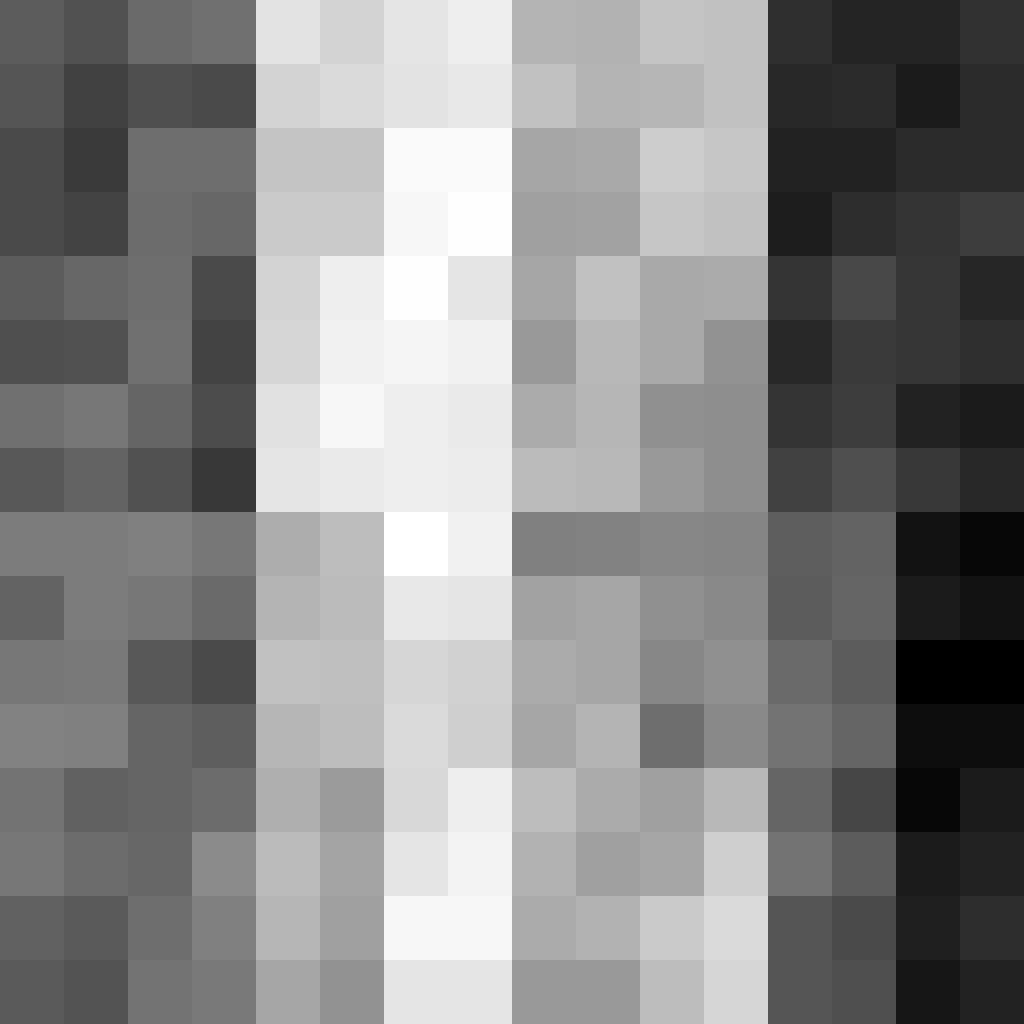
In the one-byte pattern you can clearly see some blocking - very interesting! There is clearly something going on here!

This is not a bad distribution at all for the two-byte distribution.

The three-byte pattern still sucks, argh!
At this point, I realised that we could overcome the issue of losing bits out the front of the bit shift simply by using larger integers instead of rotation:
0042 char* hash_cust7(char* s, char* d, int n){
0043 memset(d, 0, n);
0044 for(int x = 0; *s; ++x) *(int32_t*)d = (*(int32_t*)d << 3) ^ *(int32_t*)d + (d[x % n] ^= *s++);
0045 return d;
0046 }
Performance: It’s obviously much faster to use larger integers rather than the dedicated rotation function.
Collisions: We saw a nice little reduction in the number of collisions, awesome!

The one-byte pattern looks quite nice again.

The two-byte pattern is still a little blocky.
The three-byte pattern still sucks…
This was just an experiment in performing the ++x
elsewhere.
0047 char* hash_cust8(char* s, char* d, int n){
0048 memset(d, 0, n);
0049 for(int x = 0; *s;) *(int16_t*)d = (*(int16_t*)d << 5) ^ *(int16_t*)d + (d[++x % n] ^= *s++);
0050 return d;
0051 }
Performance: Runs a little slower.
Collisions: A regression in reducing collisions.
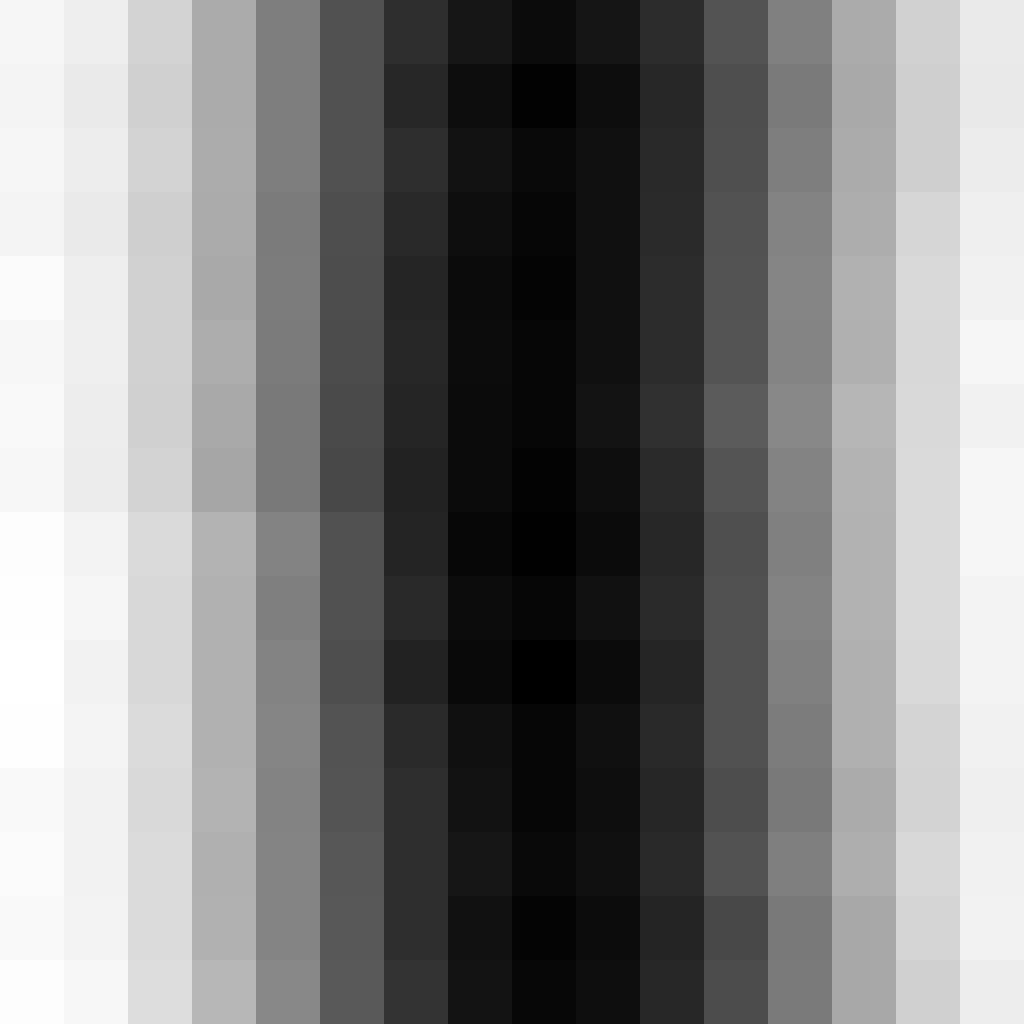
Nice one-byte pattern.

A little blocky two-byte pattern, but okay-ish.

Again an awful three-byte pattern.
At this point I was getting a little desperate, the three-byte distributions have so-far sucked! I started experimenting with purposely ensuring that the upper hash was definitely touched by our algorithm:
0052 char* hash_cust9(char* s, char* d, int n){
0053 memset(d, 0, n);
0054 for(int x = 0; *s;){
0055 *(int16_t*)d = (*(int16_t*)d << 5) ^ *(int16_t*)d + (d[++x % n] ^= *s++);
0056 *(int16_t*)(d + (x % n - 1)) ^= *(int16_t*)d << 3;
0057 }
0058 return d;
0059 }
Performance: Doing too major calculations rather than one of course had a massive impact on performance.
Collisions: This is the first time we have seen such a massive reduction in collisions!

One-byte distribution doesn’t look all so bad.

Two-byte distribution is a little blocky, but not all so bad.

The three-byte distribution is… Wait a second! That’s awesome! We have a nice spread over the entire 3-byte distribution space!
So at this point, I needed to think of a completely different
approach. I turned back to my original resource for
simple hash functions and thought it would be worth also checking out
the sdmb implementation, specifically the gawk
implementation:
0060 char* hash_cust10(char* s, char* d, int n){
0061 memset(d, 0, n);
0062 for(int x = 0; *s; ++x)
0063 *(int32_t*)d = (d[x % n] ^= *s++) + (*(int32_t*)d << 6) + (*(int32_t*)d << 16) - *(int32_t*)d;
0064 return d;
0065 }
Performance: A reduction in performance when
compared to function 9 (cust9). Still not as good as
function 4 (cust4), but I’ll take it!
Collisions: Another reduction in collisions! I believe the merit here is we see multiple ‘smears’/‘spreads’ of data across the range.

The one-byte pattern looks super cool!

That two-byte pattern is quite evenly distributed too, not bad!

And look at that three-byte pattern, that’s very nice!
We speed-up function 11 (cust11) by changing the order
of the operations (long story):
0066 char* hash_cust11(char* s, char* d, int n){
0067 memset(d, 0, n);
0068 for(int x = 0; *s; ++x)
0069 *(uint32_t*)d = (*(int32_t*)d << 16) + (*(int32_t*)d << 6) + *(int32_t*)d + (d[x % n] ^= *s++);
0070 return d;
0071 }
Performance: This gives us a little speed-up.
Collisions: Collisions are for some reason slightly higher, although the algorithm should be essentially the same for the most part.

Weird one-byte spread.

Weirder two-byte spread.

Nice three-byte spread.
Instead of bit-shifting with (*(int32_t*)d << 16),
we now just cast instead with *(int16_t*)(d + 2). We also
use 16 + 5 bit shifting rather than 16 + 6 for a slightly nicer
distribution:
0072 char* hash_cust12(char* s, char* d, int n){
0073 memset(d, 0, n);
0074 for(int x = 0; *s; ++x)
0075 *(uint32_t*)d = *(int16_t*)(d + 2) + (*(int32_t*)d << 5) + *(int32_t*)d + (d[x % n] ^= *s++);
0076 return d;
0077 }
Performance: For our effort we get significant
speed-up, out-competing funct4 once again!
Collisions: Collisions are also reduced now owing to the shifting of 16 + 5.
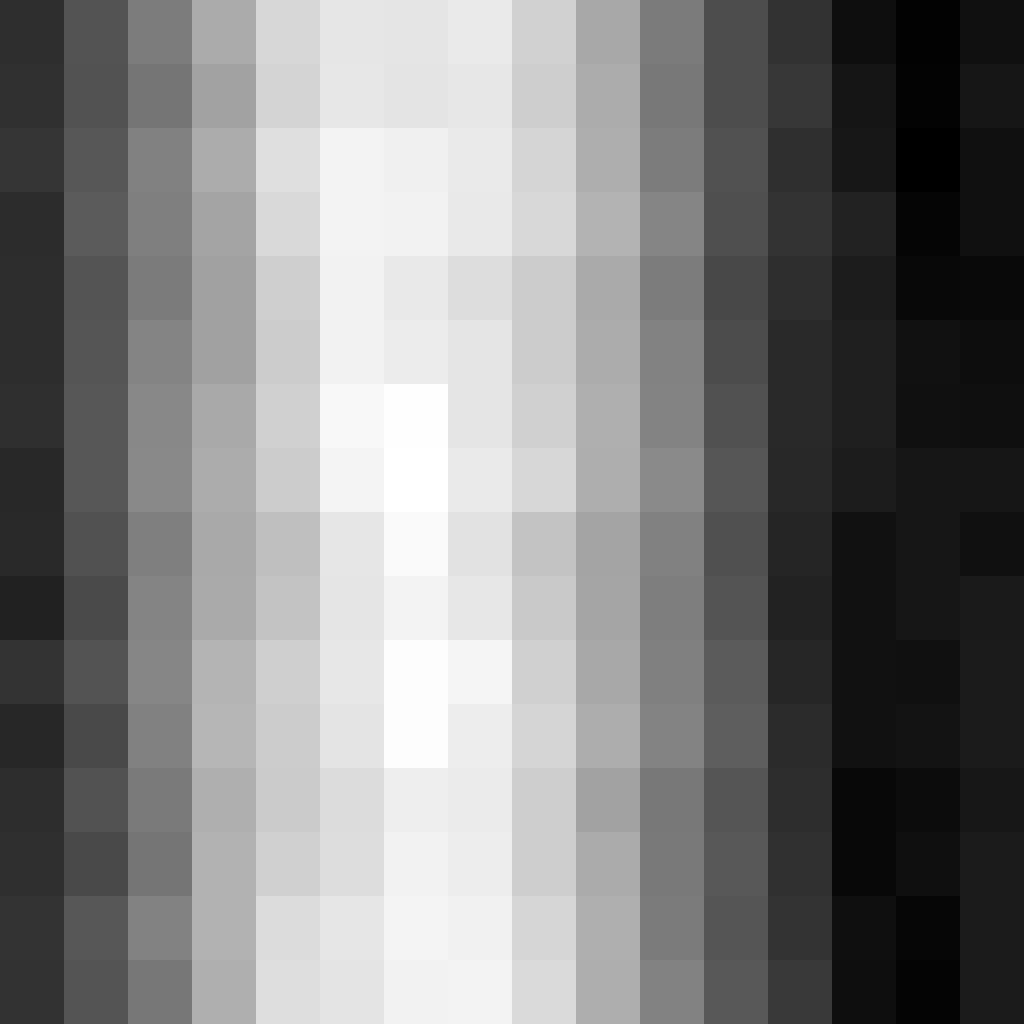
A very nice one-byte distribution.

And a very nice two-byte distribution to match.

The three-byte distribution, whilst not the prettiest to look at, is much better than previous attempts.
This function is a very small iteration of the previous function.
0078 char* hash_cust13(char* s, char* d, int n){
0079 memset(d, 0, n);
0080 for(int x = 0; *s;)
0081 *(uint32_t*)d = *(int16_t*)(d + 2) + (*(int32_t*)d << 5) + *(int32_t*)d + (d[x++ % n] ^= *s++);
0082 return d;
0083 }
Performance: Slightly better performance.
Collisions: The same number of collisions. The below exist just for completeness.
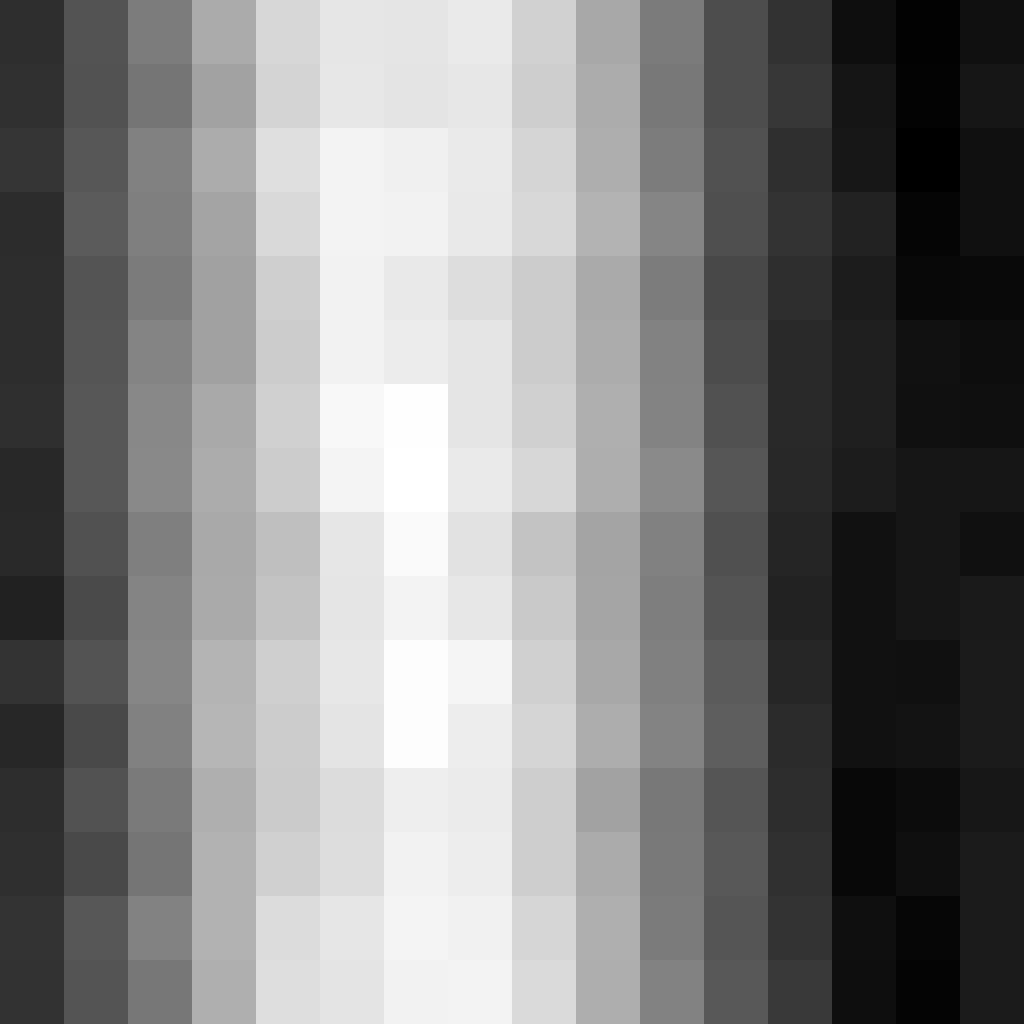


I’m pretty happy with the final implementation and believe is is a significant improvement over previous attempts. That said, I still believe there are improvements that can be made in this space:
uint8_t) addressing - Removing
the dependence on large integers is ideal. Having a hash function that
can be used on any architecture (from an 8 bit microcontroller
to a 64 bit server) and produce the same result is clearly
beneficial.memset - Ideally we do the wiping
as we setup the hash.In future experiments I will look to sample the end of the hash too when looking at the distribution. I suspect they all currently absolutely suck at filling this space in which anything and we get tonnes of collisions out there.
If you make improvements based on these tests, please let me know! Better hashes are better for everybody!