 Coffee Space
Coffee Space 
In a previous post I wrote about hash functions. I have since had some ideas regarding this and have incremented on some further algorithms to help address the distribution out in the far-end of the hashing.
The focus of this work has been to distribute the key over the entire hash space whilst maintaining reasonable performance. As far as I’m aware, this is somewhat uncharted territory.
Firstly we can look at the performance values (everything beyond function 13 is new):
| func | ms | col=8 | col=16 | col=24 | last=24 |
|---|---|---|---|---|---|
| cust1 | 2945 | 16777200 | 16776960 | 16773120 | 16777215 |
| cust2 | 3236 | 16777001 | 16773120 | 16711680 | 16777215 |
| cust3 | 3879 | 16776960 | 16711680 | 15902144 | 16777215 |
| cust4 | 3715 | 16776960 | 16711680 | 15741061 | 16777215 |
| cust5 | 3596 | 16776960 | 16711680 | 15730195 | 16777215 |
| cust6 | 3313 | 16776960 | 16711680 | 15728390 | 16777215 |
| cust7 | 3076 | 16776960 | 16711680 | 15632352 | 16777215 |
| cust8 | 2968 | 16776960 | 16711680 | 15728624 | 16777215 |
| cust9 | 3497 | 16776960 | 16711680 | 6155480 | 16777215 |
| cust10 | 3509 | 16776960 | 16711680 | 6138576 | 16777215 |
| cust11 | 3136 | 16776960 | 16711680 | 7083260 | 16777215 |
| cust12 | 2954 | 16776960 | 16711680 | 5915585 | 16777215 |
| cust13 | 2974 | 16776960 | 16711680 | 5915585 | 16777215 |
| cust14 | 3835 | 16776960 | 16754467 | 16512407 | 16773211 |
| cust15 | 7014 | 16776960 | 16711680 | 10634670 | 14805065 |
| cust16 | 4237 | 16777099 | 16775953 | 16768834 | 16777066 |
| cust17 | 3823 | 16776960 | 16711680 | 6248433 | 15886338 |
| cust18 | 7815 | 16776960 | 16711680 | 6248433 | 6606591 |
| cust19 | 6720 | 16776960 | 16711680 | 6248433 | 6425758 |
| cust20 | 6865 | 16776960 | 16711680 | 6248421 | 6605339 |
As you can see, we now look at the last three bytes collision space to get an idea of how well we distribute our values over the entire hash.
This is my initial attempt at multi-byte hashing. It’s quite convoluted and doesn’t reach the end of the hash particularly well.
0001 /* Initial implementation of multi-byte hashing */
0002 char* hash_cust14(char* s, char* d, int n){
0003 /* Copy s into d until either d filled or s length found */
0004 int l = -1;
0005 while(++l < n && s[l]) d[l] = s[l];
0006 /* If s too long, merge with existing bytes */
0007 while(s[l]) d[l % n] += s[l++];
0008 /* Finally do multi-byte merge over safe hash string */
0009 for(int x = 0; x < n;) d[x % n] = d[x % n] - (d[++x % n] << 3) + l;
0010 return d;
0011 }
Performance: This is not too bad all things considered. It’s well within the expected range.
Collisions: As you can see, there are still a significant number of collisions at the end of the hash and we lose all benefits at the start of the hash.
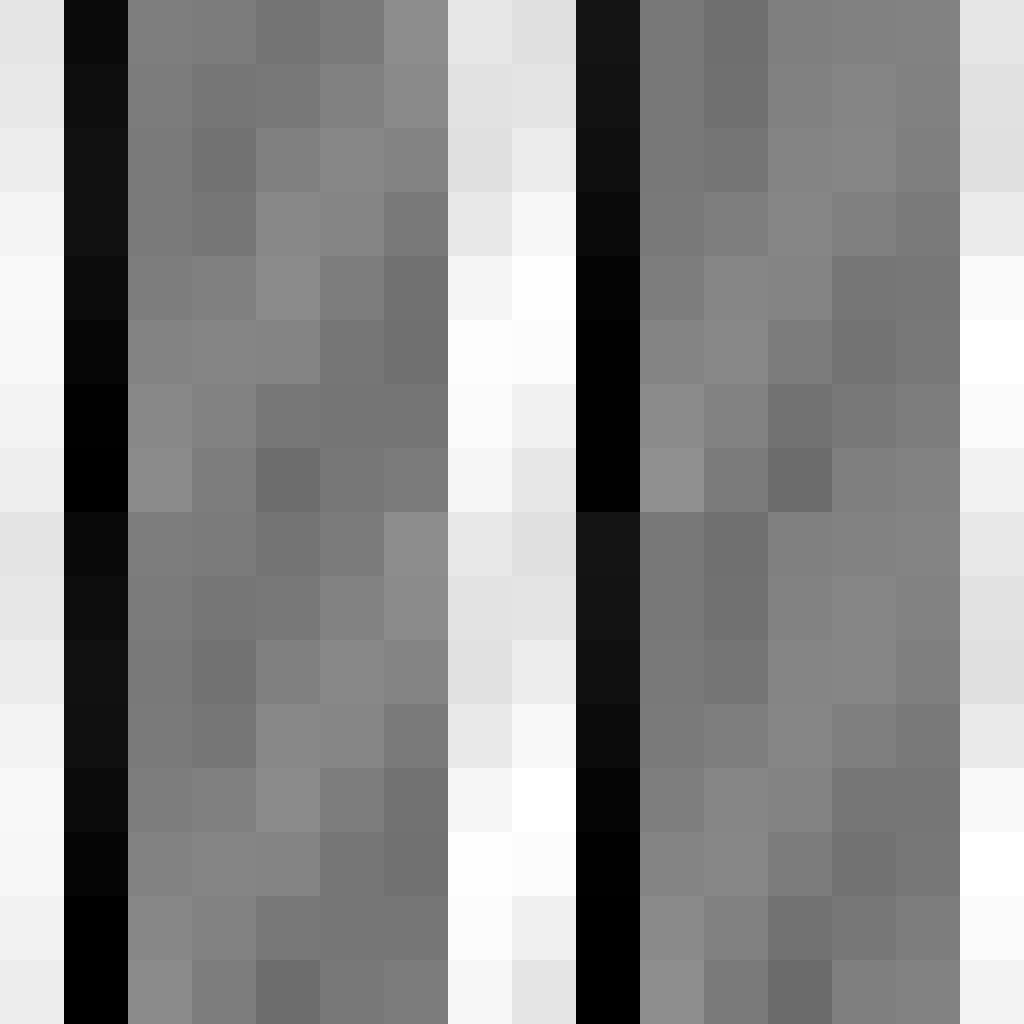
As you can see, the one byte distribution is terrible.
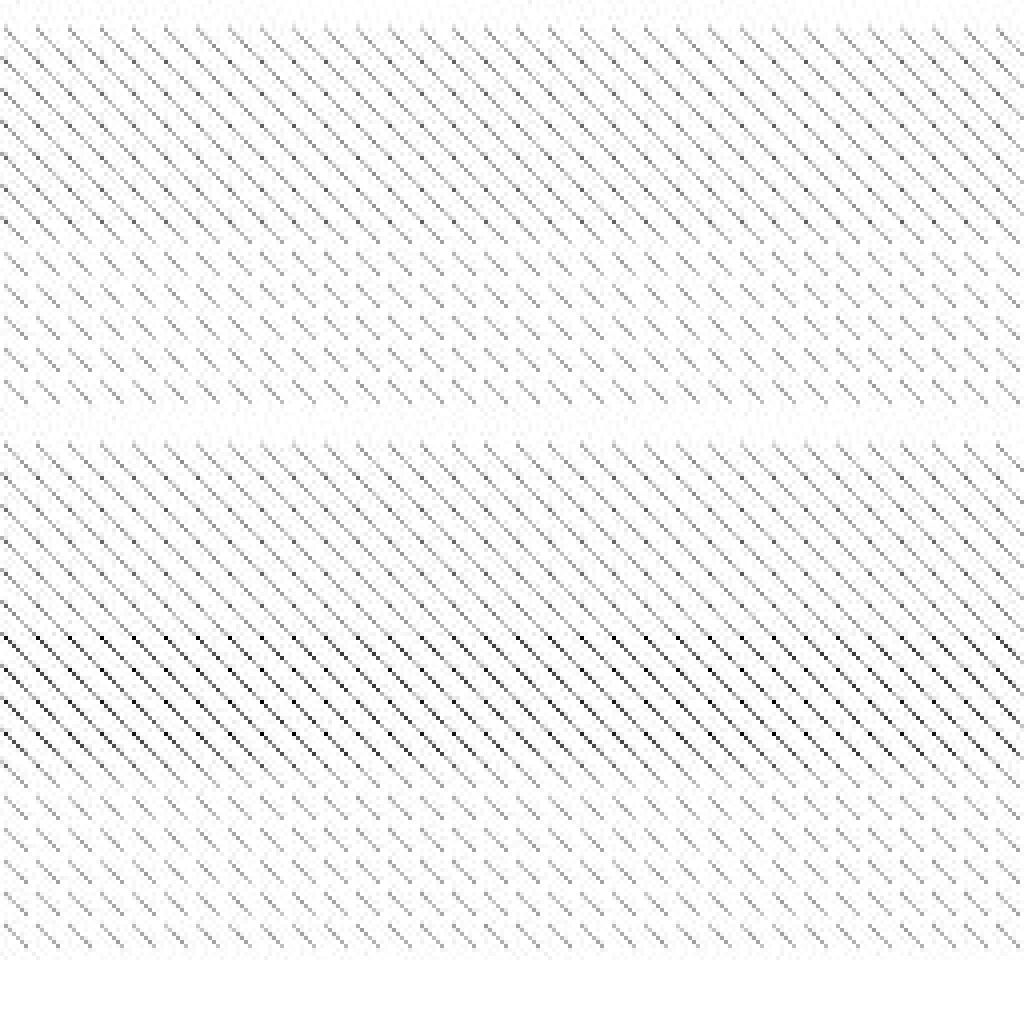
The two byte distribution is even worse.

The three byte distribution is even worse than the two byte distribution.

As you can see, the last three bytes are barely touched at all.
The idea here was to introduce an additional hashing process at the end. Again, it’s quite complicated and doesn’t work well.
0012 /* Full coverage, weak distribution, long run time */
0013 char* hash_cust15(char* s, char* d, int n){
0014 /* Copy s into d until either d filled or s length found */
0015 int l = -1;
0016 while(++l < n && s[l]) d[l] = s[l];
0017 /* Back hash */
0018 for(int x = l; s[++x];) d[x % n] ^= s[x] + l;
0019 /* Forward hash */
0020 for(char* z = d; z < d + n - 1;)
0021 *(int16_t*)z = (*(int16_t*)z << 3) ^ *(int16_t*)z ^ (d[(int)(z - d) % 2] ^= *z++);
0022 return d;
0023 }
Performance: The performance is not great. It does on the other hand begin to achieve the goal.
Collisions: The collisions are certainly much better than the previous function, but still not ideal.

One byte looks alot better.

Two byte distribution again looks better than the previous function, but it is clearly still highly predictable.

The three byte distribution is clearly predictable, but is at least represented.

The last three bytes are really not well distributed at all.
The attempt here was to experiment with single byte hashing. It did not go well, but it was at least fast.
0024 /* Faster with terrible distribution */
0025 char* hash_cust16(char* s, char* d, int n){
0026 memset(d, 0b10101010, n);
0027 /* Loop hash */
0028 int l = 0;
0029 while(*s) d[l % n] ^= *s++ ^ ++l;
0030 /* Forward hash */
0031 for(int x = 1; x < n; ++x) d[x] ^= (*d += ~d[d[x] % n] ^ l);
0032 return d;
0033 }
Performance: Performance is really quite good here.
Collisions: The collision space is exceptionally awful.
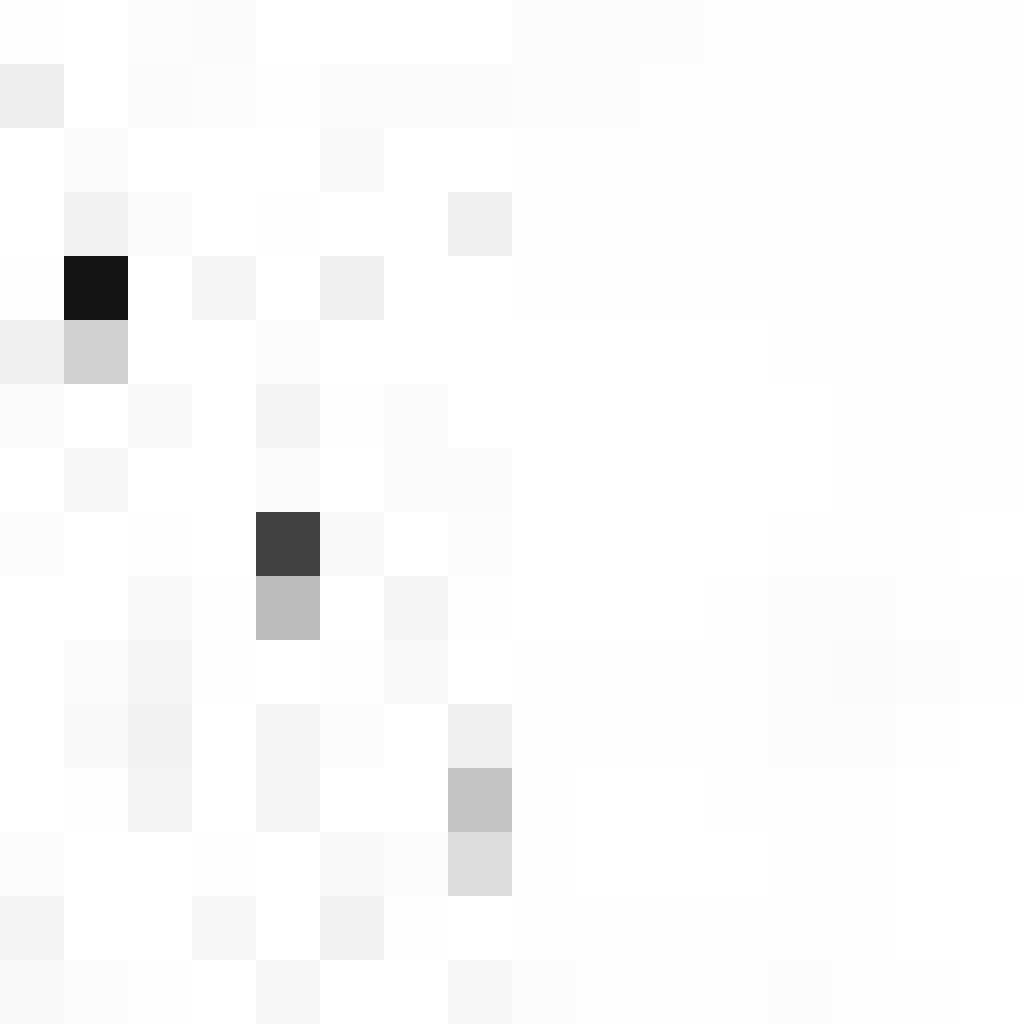
One byte is barely spread, and it only gets worse.

Two bytes clearly follows the pattern.

Three byte distribution is not represented.

The last three bytes are also not represented.
Single byte hashing was a failure, so I went back to multi-byte hashing. This experiment consists of two parses and an initial hash seed.
0034 /* Better wide distribution, better speed */
0035 char* hash_cust17(char* s, char* d, int n){
0036 memset(d, 0b10101010, n);
0037 for(int x = 0; *s;)
0038 *(uint32_t*)d = *(int16_t*)(d + 2) + (*(int32_t*)d << 5) + *(int32_t*)d + (d[x++ % n] ^= *s++);
0039 for(int x = 3; ++x < n;) d[x] = d[x] ^ d[x % 4] ^ d[x - 1];
0040 return d;
0041 }
Performance: It runs incredibly fast. If based on speed per gains, this is the best implementation.
Collisions: The distribution is really quite reasonable. We see clearly that each area of the hash has at least some reorientation.

The one byte distribution is not bad at all.

The two byte distribution is is really quite nice.

The three byte distribution we are starting to see some patterns, but in general it is also really not so bad at all.

The last three bytes have some form of pattern, but the data is at least represented reasonably out here.
With this function I took a step back, re-thought about the problem and then took another crack at it. The major change is the second part of the function, where we essential perform a second run over the hash.
0042 /* Much better distribution at the cost of computation speed */
0043 char* hash_cust18(char* s, char* d, int n){
0044 memset(d, 0b10101010, n);
0045 for(int x = 0; *s;)
0046 *(uint32_t*)d = *(int16_t*)(d + 2) + (*(int32_t*)d << 5) + *(int32_t*)d + (d[x++ % n] ^= *s++);
0047 for(int x = 3; ++x < n;)
0048 *(int16_t*)(d + x) = (*(int16_t*)(d + x) << 5) ^ *(int16_t*)(d + x) +
0049 *(int16_t*)(d + (x % 4)) + *(int16_t*)(d + x - 1);
0050 return d;
0051 }
Performance: One of the heaviest algorithms tested so far, but introduce some nice distribution.
Collisions: This is the first algorithm tested that really tackles the last three bytes (therefore the whole hash) distribution quite well.

One byte is not the best I’ve seen, but it’s passable.

The two byte is really not too bad, but acceptable.

The three byte pass is not too bad, but pretty good.

The last three bytes are very good. Look at how smooth it is!
Here we improve the distribution and improve the speed marginally.
0052 /* Slightly better distribution */
0053 char* hash_cust19(char* s, char* d, int n){
0054 memset(d, 0b10101010, n);
0055 for(int x = 0; *s;)
0056 *(uint32_t*)d = *(int16_t*)(d + 2) + (*(int32_t*)d << 5) + *(int32_t*)d + (d[x++ % n] ^= *s++);
0057 for(int x = 3; ++x < n - 1;)
0058 *(int16_t*)(d + x) = (*(int16_t*)(d + x) << 3) ^ *(int16_t*)(d + x) +
0059 (*(int16_t*)(d + (x % 4)) ^ *(int16_t*)(d + x - 1));
0060 return d;
0061 }
Performance: Runs slightly faster. This is the fastest three byte implementation so far.
Collisions: This has some of the best multi-byte distributions too.

One byte is okay, but not great.

Two bytes are not bad.

Three bytes are nice, a little wavy, meaning there is a little predictability there.

The last three bytes are quite nice, with a small pattern present.
For this implementation we look to reduce the running time a little further.
0062 /* Reduction in running time, slight reduction in tail-end distribution */
0063 char* hash_cust20(char* s, char* d, int n){
0064 memset(d, 0b10101010, n);
0065 int x = 0;
0066 while(*s)
0067 *(uint32_t*)d = *(int16_t*)(d + 2) + (*(int32_t*)d << 5) +
0068 *(int32_t*)d + (d[x++ % n] ^= *s++);
0069 for(; x < n - 1; ++x)
0070 *(int16_t*)(d + x) = (*(int16_t*)(d + x) << 3) ^ *(int16_t*)(d + x) +
0071 (*(int16_t*)(d + (x % 4)) ^ *(int16_t*)(d + x - 1));
0072 return d;
0073 }
Performance: On testing, the performance was a little worse.
Collisions: Slightly worse than the previous distribution.

Again, a familiar one byte spread.

Two bytes are also not too bad.

Three bytes we see more of the same pattern.

The last three bytes are okay, but not too great.
Function 19 is by far the best function so far for full byte distribution.
It’s still not perfect though. I wrote a tool to test it and found the following collision:
0074 $ echo "test " | ./beesum -n 16 0075 C4D5F9C5FB4ACFF95C3E189802AEA902 0076 $ echo "testtt" | ./beesum -n 16 0077 C4D5F9C5FB4ACFF95C3E189802AEA902
Future tests should measure the collisions with nearby hashes. This will require some thinking as to exactly how this can be achieved.
Additionally I still aim to make the function work faster, and with single bytes. This will of course require some thinking in order to achieve this.