 Coffee Space
Coffee Space 

Previously I discussed the “prisoner game” and wrote an experiment to gain intuition about the problem. This left me some questions and now I plan to explore those:
- How does this compare to a random search?
- Can we leverage the fact that we know that the experiment is continuing in order to search faster?
So our new additions will be a random search (which we would expect to perform worse) and a search that skips the first box it sees.
The following is the differing implementations - see the previous article for the main implementation.
0001 def search_self(boxes, check, p) : 0002 x = p 0003 while check > 0 : 0004 check -= 1 0005 if boxes[x] == p : 0006 return 1.0 0007 else : 0008 x = boxes[x] 0009 # Nothing found 0010 return 0.0
search_self() is the original implementation as per the
video’s description of the algorithm.
0011 def search_rand(boxes, check, p) : 0012 unvisited = boxes.copy() 0013 while check > 0 : 0014 check -= 1 0015 box = unvisited.pop(random.randint(0, len(unvisited) - 1)) 0016 if box == p : 0017 return 1.0 0018 # Nothing found 0019 return 0.0
search_rand() is a random search. It searched for yet
un-checked boxes, until it has checked the number of boxes allowed.
0020 def search_skip(boxes, check, p) : 0021 x = int((p + 1) % len(boxes)) 0022 while check > 0 : 0023 check -= 1 0024 if boxes[x] == p : 0025 return 1.0 0026 else : 0027 x = boxes[x] 0028 # Nothing found 0029 return 0.0
search_skip() is the same as search_self(),
but instead skips starting the search at it’s own number and starts
checking at the number number. For example, if we have prisoner 69,
instead of searching the box labelled 69, they would instead search at
box 70.
So, the results are not as expected and I believe there is something interesting at work here…
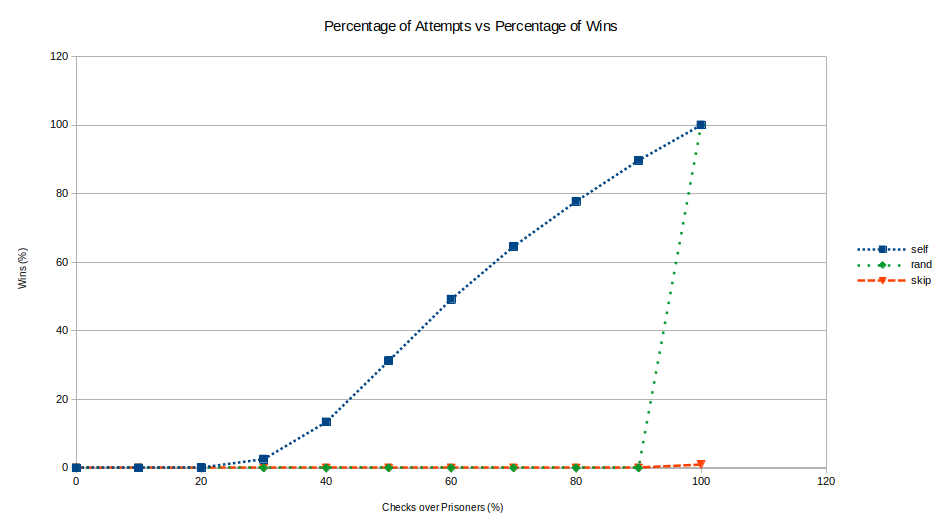
So obviously we have have our ‘self’ algorithm that works as we calculated previously.
Next we have the ‘rand’ algorithm that performs poorly, unless it is allowed to check all boxes (as expected).
Then we have the ‘skip’ algorithm that simply performs the same search as ‘self’, but skips by 1. Wait a second… It performs really badly? This was not expected at all. This indicates that the first position we start searching from affects which “loop” we end up on.
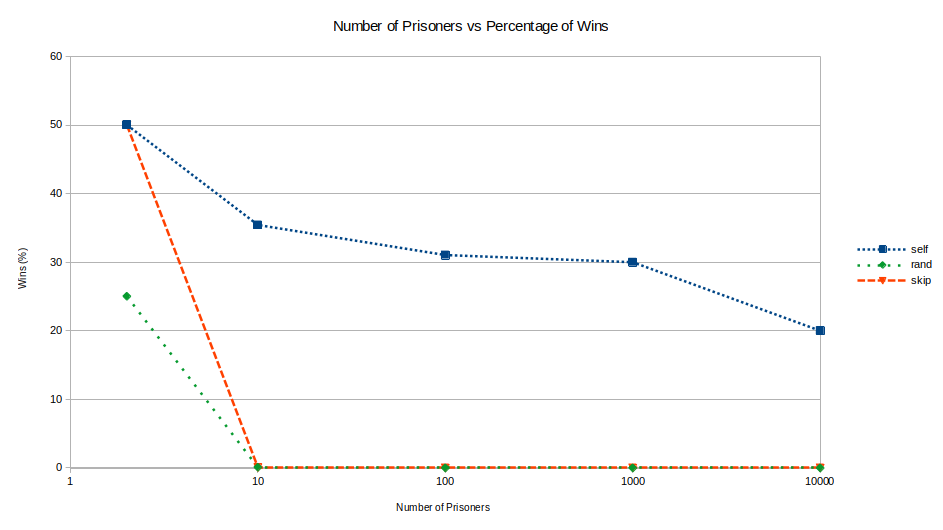
The ‘self’ and ‘rand’ algorithm performs as expected, but again the ‘skip’ algorithm performs badly.
Raw data is as follows:
0030 self,1,2,10000000,5001457.0,10000000,50.014570000000006%,20769640900 0031 self,5,10,1000000,354262.0,1000000,35.4262%,10672566808 0032 self,50,100,100000,31044.0,100000,31.044%,45544446116 0033 self,500,1000,1000,300.0,1000,30.0%,42518455906 0034 self,5000,10000,10,2.0,10,20.0%,48287585677 0035 self,0,100,100000,0.0,100000,0.0%,6767997565 0036 self,10,100,100000,0.0,100000,0.0%,14948252739 0037 self,20,100,100000,41.0,100000,0.041%,24070816482 0038 self,30,100,100000,2565.0,100000,2.565%,29847178737 0039 self,40,100,100000,13391.0,100000,13.391%,35310234124 0040 self,50,100,100000,31220.0,100000,31.22%,39331259432 0041 self,60,100,100000,49185.0,100000,49.185%,46962140164 0042 self,70,100,100000,64605.0,100000,64.605%,49379891664 0043 self,80,100,100000,77735.0,100000,77.735%,50901500812 0044 self,90,100,100000,89687.0,100000,89.687%,51604109332 0045 self,100,100,100000,100000.0,100000,100.0%,49706191336 0046 rand,1,2,10000000,2502035.0,10000000,25.02035%,39248657527 0047 rand,5,10,1000000,960.0,1000000,0.096%,43968653134 0048 rand,50,100,100000,0.0,100000,0.0%,339515429024 0049 rand,500,1000,1000,0.0,1000,0.0%,367579695702 0050 rand,5000,10000,10,0.0,10,0.0%,607923410899 0051 rand,0,100,100000,0.0,100000,0.0%,7536006420 0052 rand,10,100,100000,0.0,100000,0.0%,89803886521 0053 rand,20,100,100000,0.0,100000,0.0%,155016395627 0054 rand,30,100,100000,0.0,100000,0.0%,217018814940 0055 rand,40,100,100000,0.0,100000,0.0%,268104319902 0056 rand,50,100,100000,0.0,100000,0.0%,311205975417 0057 rand,60,100,100000,0.0,100000,0.0%,346592624045 0058 rand,70,100,100000,0.0,100000,0.0%,393477700167 0059 rand,80,100,100000,0.0,100000,0.0%,437455875647 0060 rand,90,100,100000,3.0,100000,0.003%,436822600070 0061 rand,100,100,100000,100000.0,100000,100.0%,415083683072 0062 skip,1,2,10000000,4999941.0,10000000,49.99941%,21114771236 0063 skip,5,10,1000000,549.0,1000000,0.054900000000000004%,10848657570 0064 skip,50,100,100000,0.0,100000,0.0%,40141763593 0065 skip,500,1000,1000,0.0,1000,0.0%,36626036769 0066 skip,5000,10000,10,0.0,10,0.0%,39426001437 0067 skip,0,100,100000,0.0,100000,0.0%,6327002856 0068 skip,10,100,100000,0.0,100000,0.0%,14754162746 0069 skip,20,100,100000,0.0,100000,0.0%,22457383263 0070 skip,30,100,100000,0.0,100000,0.0%,29181398259 0071 skip,40,100,100000,0.0,100000,0.0%,34925192476 0072 skip,50,100,100000,0.0,100000,0.0%,40708253132 0073 skip,60,100,100000,0.0,100000,0.0%,45181734701 0074 skip,70,100,100000,0.0,100000,0.0%,50143153485 0075 skip,80,100,100000,0.0,100000,0.0%,54583025757 0076 skip,90,100,100000,0.0,100000,0.0%,58502951878 0077 skip,100,100,100000,990.0,100000,0.9900000000000001%,63255395304
It appears that I was missing something from the original video. After re-watching, I now see my error. I initially thought after seeing this result that there was something wrong with the shuffle algorithm in Python. After re-writing my own shuffle from scratch, I realised I was missing something.
If we imagine the problem as just 4 boxes… But this time we remove the numbers entirely and just treat them as symbols.
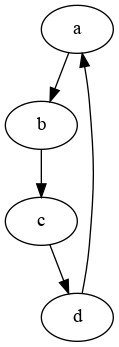
As you can see, if you were prisoner ‘a’ for example, in box ‘d’ would be your card. But you would first need to visit the box labelled ‘a’, then ‘b’, then ‘c’.
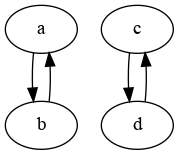
If you have a broken loop, you can always guarantee that your label will be in the same loop as the box with your number. If you were ‘a’ in this example, you visit ‘b’, which then contains your label.
With the ‘skip’ algorithm, we were essentially an ‘a’ prisoner pretending to be for example a ‘c’ and potentially joining a loop without our label in it.
Understanding! That was an interesting journey for me, I like these little problems!