 Coffee Space
Coffee Space 

I recently come across this article over on HackerNews titled ‘Strangest Sorting Algorithms’. I found the algorithms discussed there quite fun!
I decided to do some tests and have some fun with this. The following is a discussion regarding what I found out.
I’ll start with the results, and then discuss what they actually mean.
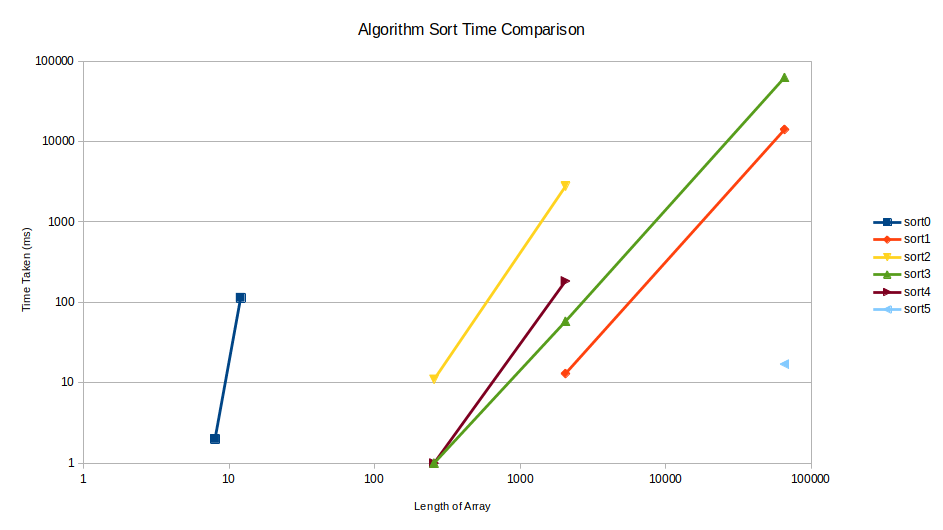
Here is a quick overview of the algorithms and the design behind them. We make the following assumptions:
sort0()So this one was more inline with the original article. For small arrays of less than 10 elements and assuming you do not want to run this sort often, it’s actually not too bad at all.
0001 /* Randomly swap, return when sorted */
0002 void sort0(int* a, int l){
0003 seed_random(0);
0004 int ordered = 0;
0005 while(ordered == 0){
0006 /* Random element */
0007 int i = rand() % l;
0008 int j;
0009 /* Random element which is not what we already selected */
0010 while((j = get_random() % l) == i);
0011 /* Swap elements */
0012 int t = a[i];
0013 a[i] = a[j];
0014 a[j] = t;
0015 /* Check if list now ordered */
0016 ordered = 1;
0017 for(int x = 1; x < l; ++x){
0018 if(a[x - 1] > a[x]){
0019 ordered = 0;
0020 break;
0021 }
0022 }
0023 }
0024 }
A use-case for this algorithm could be:
sort1()This algorithm is based on the classic bubble sort algorithm. It is ‘blind’ because it cannot end early, even if the array is already sorted. This is based on the assumption that the input array to be sorted is relatively high entropy and requires a lot of sorting, such that it’s likely most operations will be required and we can save on additional checking.
0025 /* Blind bubble sort */
0026 void sort1(int* a, int l){
0027 /* Outer pass loop */
0028 for(int pass = 0; pass < l - 1; ++pass){
0029 /* Forward iterate through list */
0030 for(int x = 1; x < l - pass; ++x){
0031 /* Compare elements and swap */
0032 if(a[x - 1] > a[x]){
0033 /* Swap elements */
0034 int t = a[x - 1];
0035 a[x - 1] = a[x];
0036 a[x] = t;
0037 }
0038 }
0039 }
0040 }
This algorithm is of course well known and does not need to be explained. The advantage of this algorithm is it has a guaranteed run time based on the number of elements.
sort2()This is the first of the “unreasonably effective” random-based shuffling algorithms. It finds an element out of order and swaps it randomly with some other element further up the array. It’s essentially a random bubble sort.
0041 /* Unreasonably effective random sorting */
0042 void sort2(int* a, int l){
0043 seed_random(0);
0044 int i = 0;
0045 while(i < l){
0046 /* Random element which is not what we already selected */
0047 int j = i + 1 + (get_random() % (l - (i + 1)));
0048 /* Swap elements */
0049 int t = a[i];
0050 a[i] = a[j];
0051 a[j] = t;
0052 /* Check if list now ordered */
0053 i = 0;
0054 while(++i < l){
0055 if(a[i - 1] > a[i]){
0056 --i;
0057 break;
0058 }
0059 }
0060 }
0061 }
This is significantly faster for such simple logic.
sort3()This is based on sort2(), but it looks to ensure that
whichever element we swap the out-of-order element with in the later
part of the list, is smaller than the element we currently have. As a
result, this random shuffle performs even better.
0062 /* Only randomly switch elements that improve the situation */
0063 void sort3(int* a, int l){
0064 seed_random(0);
0065 int i = 0;
0066 while(i < l){
0067 int j;
0068 /* Random element in higher end which is smaller than what we want to swap */
0069 while(a[j = i + 1 + (get_random() % (l - (i + 1)))] > a[i]);
0070 /* Swap elements */
0071 int t = a[i];
0072 a[i] = a[j];
0073 a[j] = t;
0074 /* Check if list now ordered */
0075 i = 0;
0076 while(++i < l){
0077 if(a[i - 1] > a[i]){
0078 --i;
0079 break;
0080 }
0081 }
0082 }
0083 }
For small arrays elements, this algorithm is significantly fast.
sort4()Surprisingly, removing the randomness from sort3()
actually slows down the algorithm!
0084 /* Deterministic search variant of sort3() */
0085 void sort4(int* a, int l){
0086 int i = 0;
0087 while(i < l){
0088 int j = l;
0089 while(a[--j] >= a[i]);
0090 /* Swap elements */
0091 int t = a[i];
0092 a[i] = a[j];
0093 a[j] = t;
0094 /* Check if list now ordered */
0095 i = 0;
0096 while(++i < l){
0097 if(a[i - 1] > a[i]){
0098 --i;
0099 break;
0100 }
0101 }
0102 }
0103 }
sort5()This is a super interesting approach called “binary search trees” (BST).
0104 struct node{ int val; struct node* left; struct node* right; };
0105
0106 void flatten(struct node* n, int* a, int* x){
0107 if(n == NULL) return;
0108 flatten(n->left, a, x);
0109 a[(*x)++] = n->val;
0110 flatten(n->right, a, x);
0111 }
0112
0113 /* Binary sort tree */
0114 void sort5(int* a, int l){
0115 struct node* nodes = malloc(sizeof(struct node) * l);
0116 int n = 0;
0117 struct node* root = &nodes[n++];
0118 root->val = a[0];
0119 root->left = NULL;
0120 root->right = NULL;
0121 for(int x = 1; x < l; x++){
0122 int v = a[x];
0123 struct node* parent = root;
0124 struct node* child = root;
0125 while(child != NULL){
0126 parent = child;
0127 if(a[x] < parent->val){
0128 child = parent->left;
0129 }else{
0130 child = parent->right;
0131 }
0132 }
0133 child = &nodes[n++];
0134 child->val = a[x];
0135 child->left = NULL;
0136 child->right = NULL;
0137 if(a[x] < parent->val){
0138 parent->left = child;
0139 }else{
0140 parent->right = child;
0141 }
0142 }
0143 int i = 0;
0144 flatten(root, a, &i);
0145 free(nodes);
0146 }
Points about this algorithm:
int) and two pointers (left and
right).A came across some interesting ideas whilst exploring this:
Note: Regarding the dimensionality of search trees, a common method is to split via spatial dimensions. Instead we could use binning to divide the problem space into artificial spatial dimensions.
The source code can be found here. Here I will discuss some details regarding what I learned from this.
Intel have RDRAND, a processor-based instruction for generating
random numbers. Seeing as a lot of our algorithms use random numbers,
one would benefit greatly from speeding these up! To compile with RDRAND
support we can use: gcc main.c -Ofast -mrdrnd -o test.
In the code, we enable random numbers by un-commenting the following:
0147 //#define RDRAND // Comment this if no RDRAND support
We generate random numbers with the following:
0148 /* Generate random number */
0149 /* NOTE: It's possible we get bad random numbers, but we care more for speed
0150 here. */
0151 int get_random(){
0152 #ifdef RDRAND
0153 /* Source: https://www.intel.com/content/www/us/en/developer/articles/guide/intel-digital-random-number-generator-drng-software-implementation-guide.html */
0154 uint16_t rand;
0155 unsigned char ok = 0;
0156 asm volatile("rdrand %0; setc %1" : "=r" (rand), "=qm" (ok));
0157 return rand;
0158 #else
0159 /* Use C implementation */
0160 return rand();
0161 #endif
0162 }
Ignoring the fact that the instruction cannot reliably return random numbers and needs to be checked to see whether it failed - it is also incredibly slow on my i7-6700HQ CPU. This was a complete waste of time.
Testing was done with the following:
0163 void test(void (*f)(int*, int), char* name, int* t, int l, int* r, int n){
0164 int* a = malloc(l * sizeof(int));
0165 memcpy(a, t, l * sizeof(int));
0166 int64_t tb = currentTimeMillis();
0167 f(a, l);
0168 int64_t te = currentTimeMillis();
0169 printf("%i\t%s\t%s\t%li\n", l, name, cmp_arr(a, l, r, n) == 0 ? "pass" : "fail", te - tb);
0170 free(a);
0171 }
As you can see, we only time how long it takes to process the sort and do not count the comparison or setup of the testing.
We also test each of the algorithms in turn, switching off some algorithms if the array length becomes too large (I only have so long to live):
0172 void run_test(char* name, int* t, int l, int* r, int n){
0173 printf("Name: '%s'\n", name);
0174 if(l <= 12) test(sort0, "sort0", t, l, r, n);
0175 test(sort1, "sort1", t, l, r, n);
0176 if(l <= 2048) test(sort2, "sort2", t, l, r, n);
0177 test(sort3, "sort3", t, l, r, n);
0178 if(l <= 2048) test(sort4, "sort4", t, l, r, n);
0179 test(sort5, "sort5", t, l, r, n);
0180 }