Coffee Space

4+ Dimensions

It is not clear how they may stack if more exist after this. Five dimensions could be represented as:

$$d = \sqrt{ g(f(x, y, z), x, y, z), (f(x, y, z) - a)^2 + (x - b)^2 + (y - c)^2 + (z - d)^2}$$

Meaning that the 5th dimension function $g()$ is some function of the lower dimensions. It could also be:

$$d = \sqrt{ g(x, y, z), (f(x, y, z) - a)^2 + (x - b)^2 + (y - c)^2 + (z - d)^2}$$

Where $g()$ is only based on three dimensions or $g()$ could equal $f()$.

Space Filling Curve

By far the more interesting idea to me is that there is one fundamental dimension, with all other dimensions being some function of this. In this case I will denote $S$ as a spatial representation, such that $S = \{ s_0, .., s_n \}$ and the rotation properties as $R = \{ r_0, .., r_n \}$. Each spatial function is also now $F = \{ f_0(), .., f_n() \}$ and each rotation function is now $G = \{ g_0(), .., g_n() \}$. This would give us:

$$d = \sqrt{ (f_0(s_0), g_0(r_0))^2 + (f_1(f_0(..), s_1), g_1(g_0(..), r_1))^2 + .. +}$$

$$\overline{(f_n(f_{n-1}(..), s_n), g_n(g_{n-1}(..), r_n))^2 }$$

It could be that there is a 4th or higher spatial dimension, but it is so diluted that it becomes undetectable compared to the first three dimensions. It is unclear what $f()$ and $g()$ may look like.

As for showing that at least two rotational properties $R$ are calculated based on one-another, see the gimbal lock problem. They are clearly not independent variables.

In terms of spatial dimensions being intertwined, it’s entirely possible there is some redundancy here too, if there is limits to each spatial axis (I think the idea of the Universe being infinitely large is insane if at some point it was condensed into single point and has not inflated infinitely fast). It’s entirely possible that the Universe is spatially some form of torus or similar type of shape where the edges wrap around on themselves.

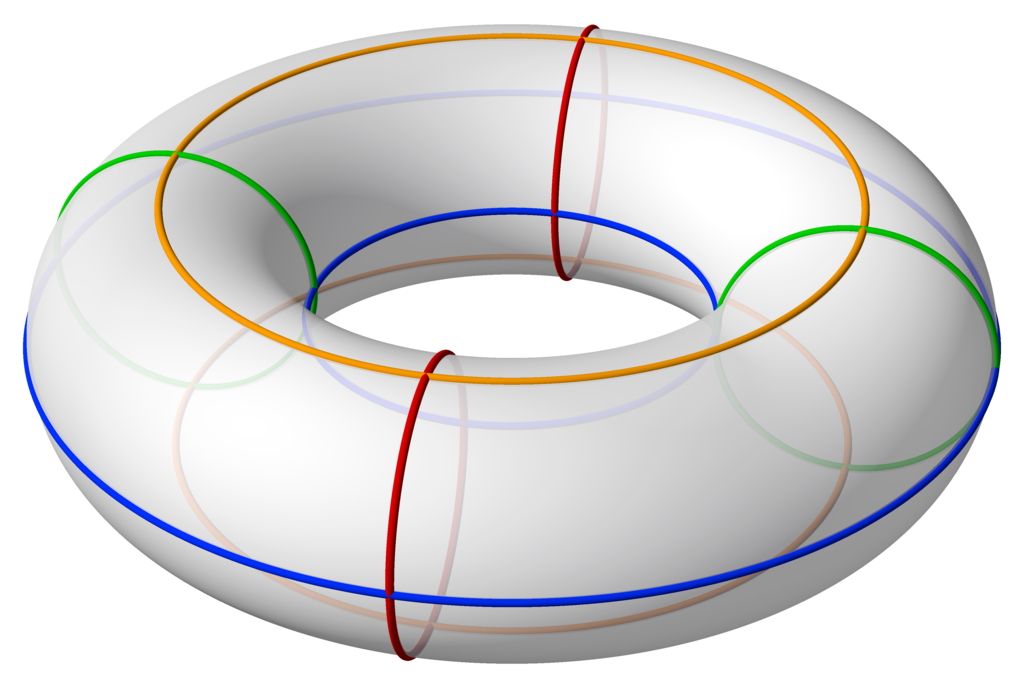
Wrapping two dimensional space would be a sphere as shown here:

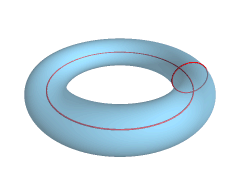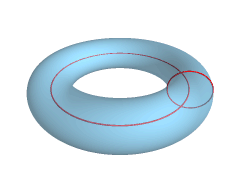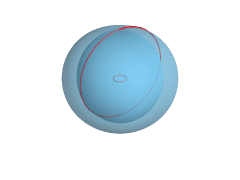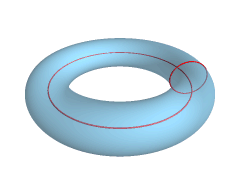
There appear to be several available options in four dimensional space, although these become increasingly difficult to both model and visualize. Something worth noting though is when we go from a 3D torus surface equation:

$$r^2 = (\sqrt{x^2 + y^2} - R)^2 + z^2$$

To a 4D Ditorus surface equation:

$$R^2 = (\sqrt{(\sqrt{x^2 + y^2} - p)^2 + z^2} -r)^2 + w^2$$

Where $R$ is the major-major radius, $r$ is the major-minor radius and $p$ is the minor-minor radius. Read more here. These can be visualized as follows:

Something to note is that some of those dimensions are more influential than others, as we increase the number of dimensions beyond four, some of the smaller spatial dimensional terms have diminishing impact to a given 3D coordinate space $(x, y, z)$. Evolution wise, it makes no sense to even begin to try and model near unobservable properties you neither have the sensors or actuators to deal with.

This would also go onto explain why effects such as quantum tunnelling can only occur mostly over small distances, and why quantum spin has little impact on over three dimensional rotation. It simply exerts too little influence. Given many particles all somewhat randomly interacting, they will mostly cancel out. I suspect the only time higher dimensions are interesting are on the super small or insanely large, where three dimensional effects have mostly cancelled (see blackholes).