 Coffee Space
Coffee Space 

Recently, I found myself wondering about writing a smaller, bare-bones operating system for the pure challenge of the task. Writing bloat software is one thing, but to write a lean thing of beauty is quite another.
There are several attractions to writing a small OS:
I am also looking into writing a book on the subject, something that people can interact with and should be a relatively small project. I feel as if most people want the experience, but don’t want to be engulfed by the art of writing an OS. I think writing a small, self-contained OS is ideal.
I have already written the Sax Operating System, with a bootloader/kernel bootloader in 512 bytes and have have come against, what I considered at the time, to be a pretty hard limit of how many features can be supported is such a small space.
This was until an idea occurred, which is where we are going with this article.
As any good scientist would, we need to analyse the data we have. We’re going to look at compressing some data we already have, in this case files from the older operating system mentioned previously. We’re going to be using the following files:
KERN Binary, AssemblyEDIT Binary, AssemblyRUN Binary, AssemblySPCE Binary, AssemblySYS Binary, AssemblyThese have been chosen as popular features from the old OS, hopefully being representative of the code we wish to write for the new OS.
The following Java code is used to analyse the binary data:
0001 import java.io.File;
0002 import java.io.FileInputStream;
0003 import java.io.IOException;
0004
0005 /**
0006 * Main.java
0007 *
0008 * This class represents the entire program, responsible for quickly analysing
0009 * binary blob data.
0010 **/
0011 public class Main{
0012 private static final String help =
0013 "\n[OPT] [FILE]..[FILE]" +
0014 "\n" +
0015 "\n OPTions" +
0016 "\n" +
0017 "\n -h --help Display this help" +
0018 "\n -v --version Display program version" +
0019 "\n" +
0020 "\n FILE" +
0021 "\n" +
0022 "\n The binary file/s to be checked.";
0023 private static final String version = "v0.0.1";
0024
0025 /**
0026 * main()
0027 *
0028 * Initialise the main program here and parse arguments to the Main object.
0029 *
0030 * @param args The arguments to the program.
0031 **/
0032 public static void main(String[] args){
0033 new Main(args);
0034 }
0035
0036 /**
0037 * Main()
0038 *
0039 * Responsible for processing the command line arguments and processing, if
0040 * required.
0041 *
0042 * @param args The arguments to the program.
0043 **/
0044 public Main(String[] args){
0045 /* Initialise variables */
0046 String[] files = null;
0047 int size = 512;
0048 /* Process command line arguments */
0049 for(int x = 0; x < args.length; x++){
0050 switch(args[x]){
0051 case "-h" :
0052 case "--help" :
0053 exit(help);
0054 break;
0055 case "-s" :
0056 case "--size" :
0057 try{
0058 size = Integer.parseInt(args[++x]);
0059 }catch(NumberFormatException e){
0060 exit(help);
0061 }
0062 break;
0063 case "-v" :
0064 case "--version" :
0065 exit(version);
0066 break;
0067 default :
0068 if(files == null){
0069 files = new String[args.length - x];
0070 }
0071 files[args.length - x - 1] = args[x];
0072 break;
0073 }
0074 }
0075 /* Make sure there is a file to process */
0076 if(files != null){
0077 /* Create the buffer */
0078 byte[] buffer = new byte[size * files.length];
0079 /* Iterate over the files */
0080 for(int x = 0; x < files.length; x++){
0081 File f = new File(files[x]);
0082 /* Make sure the file exists */
0083 if(!f.isFile()){
0084 exit(help);
0085 }
0086 /* Read the file */
0087 try{
0088 FileInputStream fis = new FileInputStream(f);
0089 fis.read(buffer, size * x, size);
0090 fis.close();
0091 }catch(IOException e){
0092 exit(help);
0093 }
0094 }
0095 /* Analyse */
0096 System.out.println("# analyse1Pairs #");
0097 analyseNPairs(buffer, 1);
0098 System.out.println("# analyse2Pairs #");
0099 analyseNPairs(buffer, 2);
0100 System.out.println("# analyse3Pairs #");
0101 analyseNPairs(buffer, 3);
0102 System.out.println("# duplicate2Pairs #");
0103 duplicateNPairs(buffer, 2);
0104 System.out.println("# duplicate3Pairs #");
0105 duplicateNPairs(buffer, 3);
0106 System.out.println("# duplicate4Pairs #");
0107 duplicateNPairs(buffer, 4);
0108 System.out.println("# nSpacing #");
0109 nSpacing(buffer);
0110 }else{
0111 exit(help);
0112 }
0113 }
0114
0115 /**
0116 * analyseNPairs()
0117 *
0118 * Analyse N pairs of bytes in the data stream.
0119 *
0120 * @param data The data to be checked.
0121 * @param n The number of pairs to be checked, where N is less than or equal
0122 * to three.
0123 **/
0124 private void analyseNPairs(byte[] data, int n){
0125 /* Initialise the frequency array */
0126 int[] freq = new int[(int)(Math.pow(256, n))];
0127 for(int x = 0; x < freq.length; x++){
0128 freq[x] = 0;
0129 }
0130 /* Iterate over the pairs, increase the frequency */
0131 for(int x = 0; x < data.length - n + 1; x++){
0132 /* Calculate the index value */
0133 int index = 0;
0134 for(int y = 0; y < n; y++){
0135 int t = (int)(data[x + (n - y - 1)]);
0136 index += Math.pow(256, y) * (t < 0 ? 127 - t : t);
0137 }
0138 /* Increase the frequency */
0139 ++freq[index];
0140 }
0141 /* Output the results */
0142 for(int x = 0; x < freq.length; x++){
0143 /* NOTE: Only print if a result greater than zero. */
0144 if(freq[x] > 0){
0145 System.out.println(x + "\t" + freq[x]);
0146 }
0147 }
0148 }
0149
0150 /**
0151 * duplicateNPairs()
0152 *
0153 * Analyse N duplicate pairs of bytes in the data stream.
0154 *
0155 * @param data The data to be checked.
0156 * @param n The number of duplicate pairs to be checked.
0157 **/
0158 private void duplicateNPairs(byte[] data, int n){
0159 /* Initialise the frequency array */
0160 int[] freq = new int[256];
0161 for(int x = 0; x < freq.length; x++){
0162 freq[x] = 0;
0163 }
0164 /* Iterate over the pairs, increase the frequency */
0165 for(int x = 0; x < data.length - n + 1; x++){
0166 /* Calculate the index value */
0167 boolean equal = true;
0168 for(int y = 1; y < n; y++){
0169 equal &= data[x] == data[x + y];
0170 }
0171 /* Check whether values are equal */
0172 if(equal){
0173 /* Increase the frequency */
0174 ++freq[((int)data[x] < 0 ? 127 - (int)data[x] : (int)data[x])];
0175 }
0176 }
0177 /* Output the results */
0178 for(int x = 0; x < freq.length; x++){
0179 /* NOTE: Only print if a result greater than zero. */
0180 if(freq[x] > 0){
0181 System.out.println(x + "\t" + freq[x]);
0182 }
0183 }
0184 }
0185
0186 /**
0187 * nSpacing()
0188 *
0189 * Analyse the frequency of which pairs can be found with N spacing.
0190 *
0191 * @param data The data to be checked.
0192 **/
0193 private void nSpacing(byte[] data){
0194 int BYTE_SIZE = 256;
0195 /* Initialise the frequency array */
0196 int[][] freq = new int[BYTE_SIZE][];
0197 for(int y = 0; y < freq.length; y++){
0198 freq[y] = new int[BYTE_SIZE];
0199 for(int x = 0; x < freq[y].length; x++){
0200 freq[y][x] = 0;
0201 }
0202 }
0203 /* Iterate over the pairs, increase the frequency */
0204 for(int o = 0; o < data.length; o++){
0205 /* Iterate over the spacing tests */
0206 for(int n = 1; n < BYTE_SIZE && n + o < data.length; n++){
0207 /* Check if current character is found after N spaces */
0208 if(data[o] == data[o + n]){
0209 ++freq[n][((int)data[o] < 0 ? 127 - (int)data[o] : (int)data[o])];
0210 }
0211 }
0212 }
0213 /* Output the results */
0214 for(int y = 0; y < freq.length; y++){
0215 for(int x = 0; x < freq[y].length; x++){
0216 /* Only print not zero results */
0217 if(freq[y][x] != 0){
0218 System.out.println(y + "\t" + x + "\t" + freq[y][x]);
0219 }
0220 }
0221 }
0222 }
0223
0224 /**
0225 * exit()
0226 *
0227 * Hard exit the program with a message.
0228 *
0229 * @param msg The message to be displayed.
0230 **/
0231 private void exit(String msg){
0232 System.out.println(msg);
0233 System.exit(0);
0234 }
0235 }
NOTE: LibreOffice graphs can be found here.
First things first, we need to find out how this binary data is distributed:
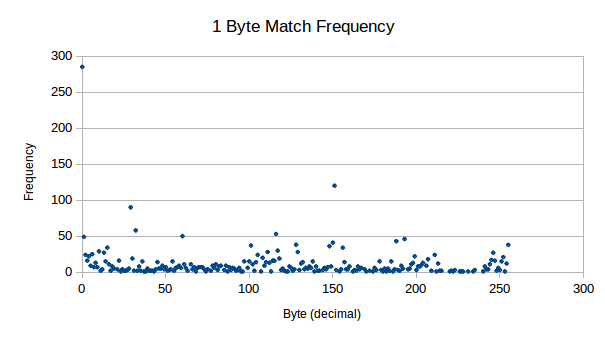
For only a little work, this is some nice results to see. Some interesting points for me:
0dFrom this, we can conclude that this is compressible data!
Here we analyse the possibility of some dictionary related lookup system, by analysing how pairs of data is distributed in our sample sets. The result is stored as a decimal, where we only keep frequencies larger than zero. This is because when originally testing the software, for some reason the Java heap doesn’t like 256 ^ 4 lookup tables, not sure why (sarcasm).
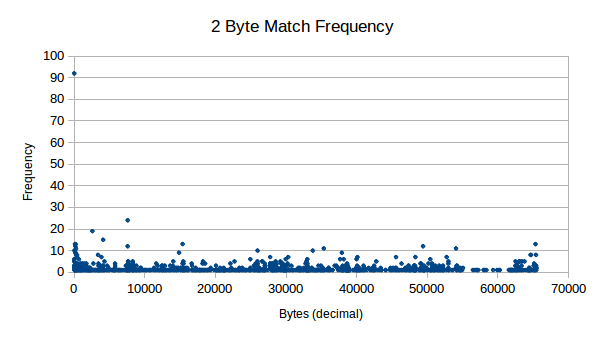
As you can see from these results, it should certainly be possible for compression on 2 byte pairs in our data, even from small 512 byte chunks.
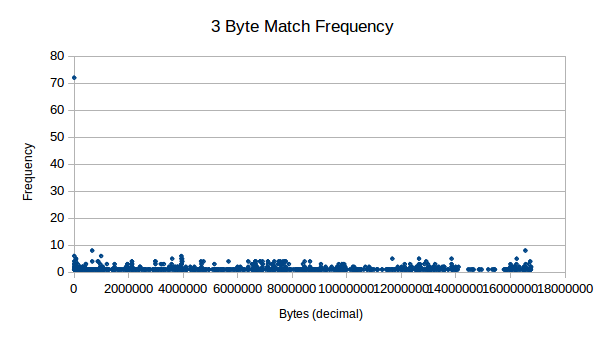
Next, we see 3 byte pairs, which also show decent levels of frequency. These don’t seem to tend much higher than “background noise” for all aspects other than 0.
In order for a dictionary method of compression to work, we can first make some assumptions about in order to theoretically test feasibility:
We can now calculate how much data we need to replace in order to make the process worth our time:
This can now be expressed as y = mx + c, or y = (3 * x) - 50. In order to break even, so that y = 0, we must calculate 50 / 3 = x, which is 17 matches. In order to save 50 bytes, comparable to the implementation of the decompression algorithm, we must calculate where y = 50, so that (50 + 50) / 3, which is 34 matches. In just 512 bytes, this is a push.
Of course, this doesn’t take into consideration the data required to describe the replacements, further eating into any gains we may have. In order for this system to work, there must be a high amount of overlapping dictionary mappings, otherwise the description of the replacement will cost more than the gain from the replacement.
Yet another interesting pattern (a subset pattern from the one discussed previously) in the data is where we see duplicates of data side-by-side with the same value. Consider the following results:

We see that firstly, we have many duplicate zeros in our data. Other than this, there are still very strong presences of duplicate data for other values, mainly for 15d, where we see 7 strong counts.
There are some benefits to duplicate representation:
On the negative side, duplicates are much less likely to occur in 125 bytes. Somewhere between 46 / 285 and 92 / 285 of our data is side-by-side zeros, representing space that we can fit more programming code in anyway. This greatly reduces the benefit of using this method.
These tables are now too small to even produce a graph that has any advantage, so we display our raw results here:
0236 Duplicate Match_Index Frequency 0237 3 0 72 0238 3 15 6 0239 4 0 65 0240 4 15 5
Specifically, byte 15d is of interest, as this byte seems highly compressible. Assuming this value is related to an opcode, 0x0F seems to be used for popping data from the stack Wikipedia. This would mean that in our code, after using one pop instruction, we are quite likely to use another - which is certainly an interesting find.
Here we decide to look at characters that repeat after N spaces, the idea being that we can compress two bytes down into one byte that describes the current character and it’s repeat location. A example of this is below:
0241 X = 'a' 2 0242 S = 'a' 'b' 'c' 'a' 'd' 0243 S' = X 'b' 'c' 'd'
So in this example, the description is that X denotes that the character 'a' exists in the place of X, but also in an offset of 2 characters. Used in the example string S, we see that we are able to compress our string to S'. In out testing, we limit the spacing to 255 spaces, as this still easily fits in an 8 bit byte and makes the data description smaller to work with.
Now we analyse the results:
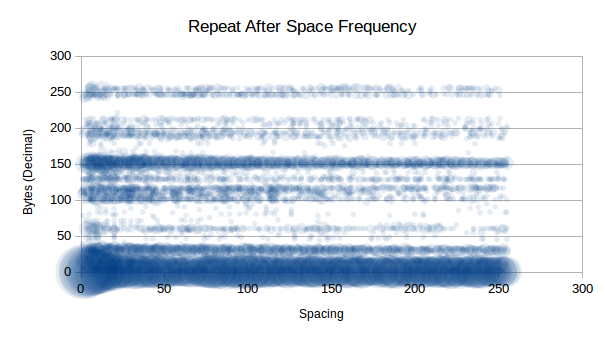
As you can see, 0d is clearly highly compressible as we saw in previous tests, but now we see that there are some other highly compressible data that don’t repeat immediately, such as 150d. Interestingly that is not an x86 instruction.
A list interesting (repeats 5 or more times) repeats include:
0d - No spacing1d - Possible VM call10d - New line13d - Carriage return15d - Pop instruction29d - No information32d - Space character or logical AND instruction60d - No information101d - No information116d - No information117d - No information150d - No information151d - No information156d - Push flags instruction188d - No information251d - Set interrupt flag instruction255d - Call or decrement or increment or jump instructionLooking past the highly compressible 0d, which will be unlikely to be in our final compression data, we the following order of compressible data (just some):
151d at 20 spaces is compressible 20 times150d at 6 spaces is compressible 16 times29d at 13 spaces is compressible 11 times60d at 4 spaces is compressible 9 times255d at 7 spaces is compressible 7 times117d at 10 spaces is compressible 7 times32d at 7 spaces is compressible 7 timesWe potentially have 31 bytes at our disposal to represent N-spaced repeats, so as long as the savings are greater than the cost of representation (<INDICATOR> + <CHAR> + <SPACING>), then we shall see savings.
Assuming we get half of the saving mentioned in our list, that would be:
0244 (20 + 16 + 11 + 9 + 7 + 7 + 7) / 2 = 38.5 ~= 38 bytes
That 38 bytes saved, minus the representation bytes, 7 * 3 = 21, leaves us a saving off 17 bytes. Of course, the implementation of the decompression also will have a cost, meaning we will use more bytes than we save with any reasonably sized OS. Back to the drawing board!
So a crazy idea I had was to implement a bubble-sort inspired compression algorithm, something that seemed on paper that may have some merit. I decided to write a program to explore the idea, so that I could approach this idea with a Scientific approach.
Here is the test program:
0245 import time
0246
0247 debug = False
0248
0249 # ordered()
0250 #
0251 # Check if the data is ordered.
0252 #
0253 # @param data The stream to be tested.
0254 # @return True if ordered, otherwise False.
0255 def ordered(data) :
0256 for x in range(0, len(data) - 1) :
0257 if data[x] > data[x + 1] :
0258 return False
0259 return True
0260
0261 # decompressed()
0262 #
0263 # Check whether the data has been decompressed.
0264 #
0265 # @param data The stream to be tested.
0266 # @return True if decompressed, otherwise False.
0267 def decompressed(data) :
0268 for x in range(0, len(data) - 1) :
0269 if data[x] == float("inf") :
0270 return False
0271 return True
0272
0273 # order()
0274 #
0275 # Orders a set of data. Functional method.
0276 #
0277 # @param data The data stream to be tested.
0278 # @return The ordered data.
0279 def comp(data) :
0280 # Initialise variables
0281 indx = 0
0282 # Infinite loop until complete
0283 while 1 :
0284 # Display what we have
0285 if debug == True :
0286 print(str(indx) + "::" + str(data))
0287 # Make sure we're not at the end
0288 if ordered(data) == True :
0289 return data
0290 # Check if we're at the end
0291 if indx >= len(data) - 1 :
0292 indx = 0
0293 # Check whether ordering required for this pair
0294 if data[indx] > data[indx + 1] :
0295 tmp = data[indx]
0296 data[indx] = data[indx + 1]
0297 data[indx + 1] = tmp
0298 data.insert(indx + 2, float("inf"))
0299 # Next check
0300 indx += 1
0301 # Should never reach here!
0302 print("ERROR!")
0303
0304 # decomp()
0305 #
0306 # Decompress the data stream. Functional method.
0307 #
0308 # @param data The data stream to be tested.
0309 # @return The unordered data.
0310 def decomp(data) :
0311 # Initialise variables
0312 indx = 0
0313 # Infinite loop until complete
0314 while 1 :
0315 # Display what we have
0316 if debug == True :
0317 print(str(indx) + "::" + str(data))
0318 # Make sure we're not at the end
0319 if decompressed(data) == True :
0320 return data
0321 # Check if we're at the end
0322 if indx <= 2 :
0323 indx = len(data) - 1
0324 # Check whether ordering required for this pair
0325 if data[indx] == float("inf") :
0326 tmp = data[indx - 1]
0327 data[indx - 1] = data[indx - 2]
0328 data[indx - 2] = tmp
0329 data.pop(indx)
0330 # Next check
0331 indx -= 1
0332 # Should never reach here!
0333 print("ERROR!")
0334
0335 tests = [
0336 [4, 2, 1, 3],
0337 [4, 3, 2, 1],
0338 [3, 4, 1, 2],
0339 [3, 2, 4, 1],
0340 [1, 2, 1, 2],
0341 [2, 1, 2, 1],
0342 [4, 2, 1, 3, 4],
0343 [4, 2, 1, 3, 4, 3],
0344 [4, 2, 1, 3, 4, 3, 2],
0345 [4, 2, 1, 3, 4, 3, 2, 1],
0346 [4, 2, 1, 3, 4, 3, 2, 1, 3],
0347 [4, 2, 1, 3, 4, 3, 2, 1, 3, 4],
0348 [4, 2, 1, 3, 4, 3, 2, 1, 3, 4, 1],
0349 [4, 2, 1, 3, 4, 3, 2, 1, 3, 4, 1, 2],
0350 [4, 2, 1, 3, 4, 3, 2, 1, 3, 4, 1, 2, 3]
0351 ]
0352
0353 print("TEST,INITIAL_SIZE,START_TIME,DEFLATED_SIZE,COMPRESSION_TIME,DECOMPRESSION_TIME,RESULT")
0354 for x in range(0, len(tests)) :
0355 output = "\"" + str(tests[x]) + "\","
0356 output += str(len(tests[x])) + ","
0357 output += str(time.time()) + ","
0358 c = comp(tests[x])
0359 output += str(len(c)) + ","
0360 output += str(time.time()) + ","
0361 d = decomp(c)
0362 output += str(time.time()) + ","
0363 if c == d :
0364 output += "EQUAL"
0365 else :
0366 output += "NOT_EQUAL"
0367 # Output the results
0368 print(output)
This produced the following results (original here):
0369 SIZE DEFLATE COMPRESS DECOMPRESS 0370 4 15 0 0 0371 4 21 0 0 0372 4 13 0 0 0373 4 15 0 0 0374 4 6 0 0 0375 4 11 0 0 0376 5 27 0 0 0377 6 53 0 0 0378 7 116 0.0099999905 0 0379 8 289 0.0700001717 0 0380 9 574 0.6699998379 0 0381 10 1140 4.9600000381 0.0099999905 0382 11 2526 46.3900001049 0.0199999809 0383 12 5105 522.2400000095 0.129999876 0384 13 10206 5851.7400000095 0.7999999523
Now we can now take a look at the feasibility of the project and whether we are looking at a good compression method or if this is not feasible.
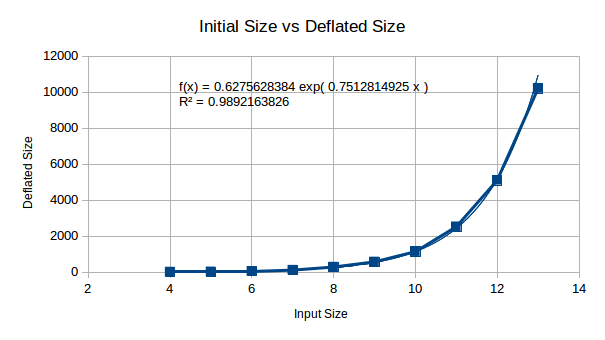
Here we are looking at initial size vs deflated size, the purpose of this is to look at RAM usage from decompression. This doesn’t initially look too bad, until you plug in x = 512 (512 bytes to compress), giving you ~1x10^167… Oh my, this is a good start. We won’t stop here, there may be some technique to compress this is RAM during decompression - so we shan’t worry too much about this.
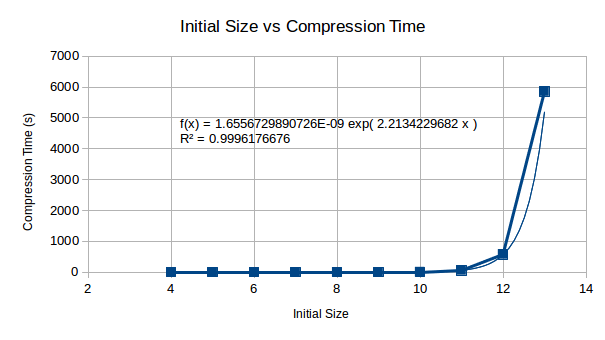
This is a show stopper - it looks as if no current computer could even compress 512 bytes using this method, in some human feasible time. By the looks of this, it could literally take a lifetime to compute the compressed data set.
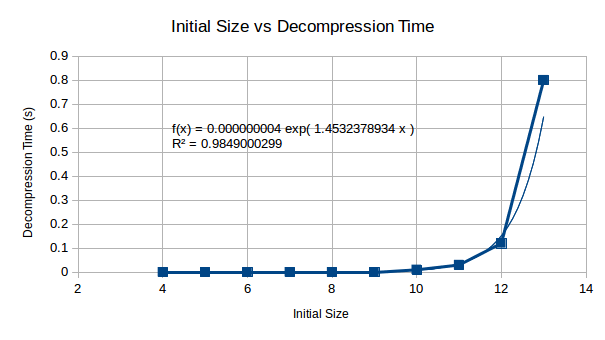
The decompression starts with small values, but appears as though it too would become an extremely time consuming process wants extended to 512 bytes worth. The following graph allows us to make a decision as to whether this will be an issue for us.
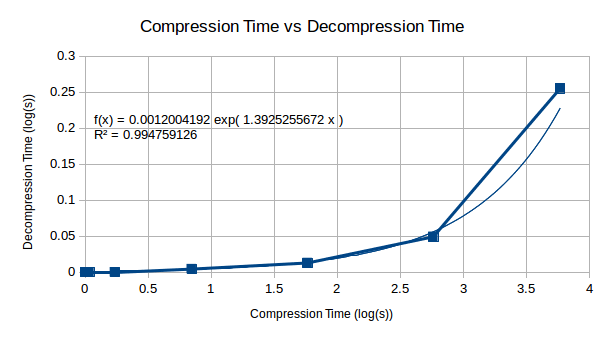
Looking at the relationship between compression and decompression, we see that compression becomes a much harder problem than decompression. This suggests that although the compression complexity is high for this algorithm, decompression will become less complex in comparison and may be computable on a reasonably well powered machine.
To conclude, there are two major problems with this compression algorithm that make it useless until solved:
It looks as though, for now, this one is off the table until a later date. This is why we test ;)
Tasks:
[X] Analyse frequency of bytes[X] Analyse frequency of 2-pair repeat bytes[X] Analyse frequency of 3-pair repeat bytes[X] Analyse duplicate frequency of 2-pair repeat bytes[X] Analyse duplicate frequency of 3-pair repeat bytes[X] Analyse duplicate frequency of 4-pair repeat bytes[X] Analyse N spacing repeat frequency[ ] Research compression algorithms[~] Design compression algorithms